HT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 2 2023
a: \(\dfrac{2x^4-3x^3+4x^2+1}{x^2-1}=\dfrac{2x^4-2x^2-3x^3+3x+6x^2-6-3x+7}{x^2-1}\)
\(=2x^2-3x+6+\dfrac{-3x+7}{x^2-1}\)
Để dư bằng 0 thì -3x+7=0
=>x=7/3
b: \(\dfrac{x^5+2x^4+3x^2+x-3}{x^2+1}\)
\(=\dfrac{x^5+x^3+2x^4+2x^2-x^3-x+x^2+1+2x-4}{x^2+1}\)
\(=x^3+2x^2-x+1+\dfrac{2x-4}{x^2+1}\)
Để đư bằng 0 thì 2x-4=0
=>x=2
19 tháng 10 2021
Bài 3:
Ta có: \(2n^2+n-7⋮n-2\)
\(\Leftrightarrow2n^2-4n+5n-10+3⋮n-2\)
\(\Leftrightarrow n-2\in\left\{1;-1;3;-3\right\}\)
hay \(n\in\left\{3;1;5;-1\right\}\)
AH
Akai Haruma
Giáo viên
18 tháng 11 2021
Lời giải:
Ta có:
$2x^4-3x^3-3x-2=2x^2(x^2-1)-3x(x^2-1)+2x^2-6x-2$
$=(2x^2-3x)(x^2-1)+2(x^2-1)-6x$
$=(2x^2-3x+2)(x^2-1)-6x$
Vậy $2x^4-3x^3-3x-2$ chia $x^2-1$ dư $-6x$
Không có đáp án nào đúng
CM
2 tháng 7 2018
Ta có
( 2 x 4 – 3 x 3 + x 2 ) : - 1 2 x 2 + 4 ( x – 1 ) 2 = 0 ⇔ 2 x 4 : ( - 1 2 x 2 ) - 3 x 3 : ( - 1 2 x 2 ) + x 2 : ( - 1 2 x 2 ) + 4 ( x 2 - 2 x + 1 ) = 0 ⇔ - 4 x 2 + 6 x – 2 + 4 x 2 – 8 x + 4 = 0
ó -2x + 2 = 0
ó x = 1
Đáp án cần chọn là: C
19 tháng 12 2021
Bài 1:
a: \(=\dfrac{2x^4-8x^3+2x^2+2x^3-8x^2+2x+18x^2-72x+18+56x-15}{x^2-4x+1}\)
\(=2x^2+2x+18+\dfrac{56x-15}{x^2-4x+1}\)
22 tháng 12 2021
b: \(=\dfrac{2x^4-2x^3-2x^2-3x^3+3x^2+3x+x^2-x-1}{x^2-x-1}\)
\(=2x^2-3x+1\)
PT
1
DM
1
27 tháng 12 2016
Ta có: \(\left(15x-6x+7\right):\left(2x+1\right)=5\)
Áp dụng định lý Bozout, ta có:
\(f\left(\frac{-1}{2}\right)=15\cdot\frac{-1}{2}-6\cdot\frac{-1}{2}+7=\frac{5}{2}\)
Vậy số dư là 2,5
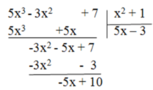
\(\dfrac{2x^4-3x^3+4x^2+1}{x^2-1}\)
\(=\dfrac{2x^4-2x^2-3x^3+3x+6x^2-6-3x+7}{x^2-1}\)
\(=2x^2-3x+6+\dfrac{-3x+7}{x^2-1}\)
Để đây là phép chia hết thì -3x+7=0
hay \(x=\dfrac{7}{3}\)