Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. \(x=\left\{4;9;16\right\}\)
b. \(x=1\)
c. \(x=\left\{-2;-1\right\}\)

a.
\(\Leftrightarrow2x^2\ge3\Leftrightarrow x^2\ge\dfrac{3}{2}\Rightarrow\left[{}\begin{matrix}x\ge\sqrt{\dfrac{3}{2}}\\x\le-\sqrt{\dfrac{3}{2}}\end{matrix}\right.\)
b.
\(\Leftrightarrow\left(1-x\right)\left(x-3\right)\ge0\Rightarrow1\le x\le3\)
c.
\(\Leftrightarrow\sqrt{1-3x}\le2-x\Leftrightarrow\left\{{}\begin{matrix}1-3x\ge0\\2-x\ge0\\1-3x\le x^2-4x+4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le\dfrac{1}{3}\\x\le2\\x^2-x+3\ge0\end{matrix}\right.\) \(\Leftrightarrow x\le\dfrac{1}{3}\)

a, \(\left(x-3\right)\left(x^2+x-20\right)\ge0\)
\(\Leftrightarrow\) \(\left(x-3\right)\left(x-4\right)\left(x+5\right)\ge0\)
+) \(x-3=0\Leftrightarrow x=3\); \(x-4=0\Leftrightarrow x=4\); \(x+5=0\Leftrightarrow x=-5\)
+) Lập trục xét dấu f(x) (Bạn tự kẻ trục nha)
\(\Rightarrow\) Bpt có tập nghiệm S = \(\left[-5;3\right]\cup\) [4; \(+\infty\))
b, \(\dfrac{x^2-4x-5}{2x+4}\ge0\)
\(\Leftrightarrow\) \(\dfrac{\left(x-5\right)\left(x+1\right)}{2x+4}\ge0\)
+) \(x-5=0\Leftrightarrow x=5\); \(x+1=0\Leftrightarrow x=-1\); \(2x+4=0\Leftrightarrow x=-2\)
+) Lập trục xét dấu f(x)
\(\Rightarrow\) Bpt có tập nghiệm S = (-2; -1] \(\cup\) [5; \(+\infty\))
c, \(\dfrac{-1}{x^2-6x+8}\le1\)
\(\Leftrightarrow\) \(\dfrac{\left(x-3\right)^2}{\left(x-4\right)\left(x-2\right)}\ge0\)
+) \(x-3=0\Leftrightarrow x=3\); \(x-4=0\Leftrightarrow x=4\); \(x-2=0\Leftrightarrow x=2\)
+) Lập trục xét dấu f(x)
\(\Rightarrow\) Bpt có tập nghiệm S = (\(-\infty\); 2) \(\cup\) (4; \(+\infty\))
Chúc bn học tốt!

Bài 1:
a: \(\Leftrightarrow x^2-5x+6< =0\)
=>(x-2)(x-3)<=0
=>2<=x<=3
b: \(\Leftrightarrow\left(x-6\right)^2< =0\)
=>x=6
c: \(\Leftrightarrow x^2-2x+1>=0\)
\(\Leftrightarrow\left(x-1\right)^2>=0\)
hay \(x\in R\)

Bài 2:
a: =>2x^2-4x+1=x^2+x+5
=>x^2-5x-4=0
=>\(x=\dfrac{5\pm\sqrt{41}}{2}\)
b: =>11x^2-14x-12=3x^2+4x-7
=>8x^2-18x-5=0
=>x=5/2 hoặc x=-1/4

Chọn D
+Ta có
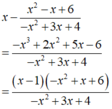
+ lại có: -x2+x+6= 0 khi x=-2 hoặc x = 3;
-x2+3x=4= 0 khi x= -1 hoặc x= 4
Bảng xét dấu
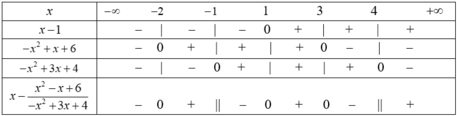
Suy ra f(x) > 0 khi và chỉ khi
![]()
Và f(x) < 0 khi và chỉ khi
![]()
a: \(x^2-3x+2=0\)
=>(x-2)(x-1)=0
=>x=2 hoặc x=1
b: 2x+6>0
=>2x>-6
hay x>-3
c: \(x^2+4x+5=0\)
\(\text{Δ}=4^2-4\cdot1\cdot5< 0\)
Do đó: Phương trình vô nghiệm
\(a,\) \(x^2-3x+2=0\) có \(2\) nghiệm \(x=1;x=3\)
\(\Rightarrow D=\left\{1;3\right\}\)
\(b,\) \(2x+6>0\) \(\Leftrightarrow x>-3\)
\(\Rightarrow\) \(D=\left\{-3;+\infty\right\}\)
\(c,\) \(x^2+4x+5=0\Leftrightarrow\left(x+2\right)^2+1=0\) \(\Rightarrow ptvn\)
\(\Rightarrow\) \(D=\varnothing\)