Tìm x biết: x thuộc Z và ( x 2 - 5 ) . ( x 2

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Pham Trong Bach

22 tháng 8 2019

Tìm x biết: x thuộc Z và ( x 2 - 5 ) . ( x 2 - 24 ) < 0

#Toán lớp 6

Cao Minh Tâm

22 tháng 8 2019

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Đinh Thị Thu Hương

25 tháng 2 2020 - olm

tìm x biết x thuộc Z và (x^2 - 5). (x^2 - 24) < 0

#Toán lớp 6

Yêu nè

25 tháng 2 2020

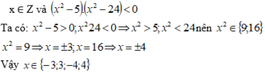
Ta có \(\left(x^2-5\right)\left(x^2-24\right)< 0\)

\(\Leftrightarrow\hept{\begin{cases}x^2-5>0\\x^2-24< 0\end{cases}}\) hoặc \(\hept{\begin{cases}x^2-5< 0\\x^2-24>0\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}x^2>5\\x^2< 24\end{cases}}\)hoặc \(\hept{\begin{cases}x^2< 5\\x^2>24\end{cases}}\) ( vô lí)

\(\Leftrightarrow5< x^2< 24\)

Mà x nguyên <=> \(x^2\in\left\{9;16\right\}\)

\(\Leftrightarrow x\in\left\{-3;-4;3;4\right\}\)

Vậy \(x\in\left\{-3;-4;3;4\right\}\)

K chắc trình bày

@@ Học tốt

Đúng(0)

Nguyễn Minh Huyền

11 tháng 1 2017 - olm

1. Tìm x thuộc Z biết (x^2 -17)(x^2 - 35)<0

2.Tìm a,b thuộc Z biết a.b=24 và a+b=10

3.Tìm các cặp số có tổng = tích

#Toán lớp 6

Chapi Beauty

23 tháng 1 2017 - olm

Giải đầy đủ hộ mình nhé :

Bài 1: Tìm x,y,;biết

a, x+y=2

b,y+z=3

c,z+x=-5

Bài 2 : Tìm x,y thuộc Z, biết (x-3).(y+2)=-5

Bài 3 : Tìm a thuộc Z, biết a.(a+2)<0

Bài 4 : Tìm x thuộc Z, sao cho (x^{2 -}4).(x²-10)<0

Bài 5 Tìm x thuộc Z, biết (x²-1).(x²-4)<0

#Toán lớp 6

Ayatocute

23 tháng 1 2017

bài 2: (x-3).(y+2) = -5

Vì x, y \(\in\)Z => x-3 \(\in\)Ư(-5) = {5;-5;1;-1}

Ta có bảng:

x-3	5	-5	-1	1
y+2	1	-1	-5	5
x	8	-2	2	4
y	-1	-3	-7	3

bài 3: a(a+2)<0

TH1 : \(\orbr{\begin{cases}a< 0\\a+2>0\end{cases}}\)=>\(\orbr{\begin{cases}a< 0\\a>-2\end{cases}}\)=> -2<a<0 ( TM)

TH2: \(\orbr{\begin{cases}a>0\\a+2< 0\end{cases}}\Rightarrow\orbr{\begin{cases}a>0\\a< -2\end{cases}}\Rightarrow loại\)

Vậy -2<a<0

Đúng(0)

Ayatocute

23 tháng 1 2017

Bài 5: \(\left(x^2-1\right)\left(x^2-4\right)< 0\)

TH 1 : \(\hept{\begin{cases}x^2-1>0\\x^2-4< 0\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x^2>1\\x^2< 4\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x>1\\x< 2\end{cases}}\)\(\Rightarrow\)1 < a < 2

TH 2: \(\hept{\begin{cases}x^2-1< 0\\x^2-4>0\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x^2< 1\\x^2>4\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x< 1\\x>2\end{cases}}\)\(\Rightarrow\)loại

Vậy 1<a<2

Đúng(1)

Nguyễn Thị Minh Ánh

9 tháng 1 2017 - olm

tìm x,y thuộc Z ,biêt: (2x-1).(2x+1)=-35

tìm c,y thuộc Z , biết: (x+1)^2 + (y+1)^2 + (x-y)^2 =2

tìm x,y thuộc Z, biết: (x^2-8).(x^2-15)<0

tìm x,y thuộc Z biết: x=6.y và|x|-|y|=60

tìm a,b thuộc Z biết: |a|+|b|<2

#Toán lớp 6

Đỗ Ngọc Tường Quyên

9 tháng 3 2018 - olm

1) Tìm x,y,z thuộc Z biết: -1/2<x/24<y/12<z/8<-1/3

2) Tìm x,y thuộc Z biết: x-2/3=1/y+1 và x+7<0, y khác 1

3) Tìm 2 phân số có mẫu bằng 9; các tử là hai số tự nhiên liên tiếp sao cho phân số 4/7 nằm giữa hai phân số đó

#Toán lớp 6

nguyễn huy hoàng

14 tháng 2 2020 - olm

bài 1:tìm x thuộc Z biết

a,|x+2|lớn hơn hoặc bằng 5

b,|x+1|>2

bài2 tìm x thuộc Z biết

a,|x-1|-x+1=0

b,|2-x|-2=x

c,|x+7|=|x-9|

bài 3:tìm x thuộc Z biết

a,|x+25|+|-y+5|=0

b,|x-40|+|x-y+10|lớn hơn hoặc bằng 0

#Toán lớp 6

Trần Hạnh Trang

14 tháng 2 2020

Bài 2:

a, |x-1| -x +1=0

|x-1| = 0-1+x

|x-1| = -1 + x

\(\orbr{\begin{cases}x-1=-1+x\\x-1=1-x\end{cases}}\)

\(\orbr{\begin{cases}x=-1+x+1\\x=1-x+1\end{cases}}\)

\(\orbr{\begin{cases}x=x\\x=2-x\end{cases}}\)

x = 2-x

2x = 2

x = 2:2

x=1

b, |2-x| -2 = x

|2-x| = x+2

\(\orbr{\begin{cases}2-x=x+2\\2-x=2-x\end{cases}}\)

2-x = x+2

x+x = 2-2

2x = 0

x = 0

Đúng(0)

nguyễn thảo nhi

14 tháng 10 2021

kkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkk

Đúng(0)

Nguyễn Thị Lan

18 tháng 1 2016 - olm

Câu 2: Tìm n thuộc Z sao cho n-1 chia hết cho n+5 mà n+5 chia hết cho n-1

Câu 3: Tìm x thuộc Z biết : (x+5).(3x-12) lớn hơn 0

Câu 4: Tìm x và y thuộc Z biết (x-7).(xy+1)=3

Câu 5: Tìm a và b thuộc Z biết : ab=a-b

#Toán lớp 6

NGUYEN ANH

1 tháng 4 2019 - olm

Tìm x biết: x thuộc số nguyên và ( x² - 5 ). ( x²- 24 ) < 0.

#Toán lớp 6

Nguyễn Linh Chi

1 tháng 4 2019

\(\left(x^2-5\right)\left(x^2-24\right)< 0\)

TH1: \(\hept{\begin{cases}x^2-5< 0\\x^2-24>0\end{cases}\Leftrightarrow\hept{\begin{cases}x^2< 5\\x^2>24\end{cases}}}\)loại

TH2: \(\hept{\begin{cases}x^2-5>0\\x^2-24< 0\end{cases}\Leftrightarrow\hept{\begin{cases}x^2>5\\x^2< 24\end{cases}\Leftrightarrow}5< x^2< 24}\)(1)

Vì x là số nguyên nên x^2 là số chín phương thỏa mãn (1)

nên x^2 bằng 9 hoặc x^2 bằng 16

\(x^2=9\Leftrightarrow x=\pm3\)

\(x^2=16\Leftrightarrow x=\pm4\)

Vậy...

Đúng(0)

l҉o҉n҉g҉ d҉z҉

4 tháng 8 2020

\(\left(x^2-5\right)\left(x^2-24\right)< 0\)

Xét 2 trường hợp

1.\(\hept{\begin{cases}x^2-5< 0\\x^2-24>0\end{cases}}\Rightarrow\hept{\begin{cases}x^2< 5\\x^2>24\end{cases}}\)( loại )

2. \(\hept{\begin{cases}x^2-5>0\\x^2-24< 0\end{cases}}\Rightarrow\hept{\begin{cases}x^2>5\\x^2< 24\end{cases}}\Rightarrow5< x^2< 24\)( nhận )

Vì x là số nguyên => x² là một số chính phương

=> \(\orbr{\begin{cases}x^2=9\\x^2=16\end{cases}}\)

=> \(\orbr{\begin{cases}x=\pm3\\x=\pm4\end{cases}}\)

Vậy \(x\in\left\{\pm3;\pm4\right\}\)

Đúng(0)

Hữu Cát

19 tháng 1 2017 - olm

Bài 1: tìm x thuộc Z biết:
a)(15-x)(-4-x)<0
b)(x-2)(7-x)>0
c)(x^2-13)(x^2=17)<0
Bài 2: Tìm a;b thuộc Z biết:
a.b=12 và a+b=-7

#Toán lớp 6

Vũ Như Mai

19 tháng 1 2017

Bài 1: Cho từng cái < hoặc > 0 rồi giải ra tìm điều kiện của x

Bài 2:

Phân tích số 12 ra là:

3 x 4 = 12

-3 x (-4) = 12

Ta thấy:

3 + 4 = 7

-3 + (-4) = -7 (đáp ứng đúng yêu cầu đề)

=> a = -3 và b = -4

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP