K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NK
1
23 tháng 5 2017
1/53+-1/106+-1/159=|x|/318
6/318+-3/318+-2/318=|x|/318
1/318=|x|/318
=>|x|=1
x=1 hoặc x=-1
NT
0
HQ
3
TN
7 tháng 6 2016
Giả sử x, y là các số nguyên thoả mãn (1). Ta thấy 159 và 3x đều chia hết cho 3 nên 17y cũng chia hết cho 3, do đó y chia hết cho 3 ( vì 17 và 3 nguyên tố cùng nhau)
Đặt y = 3t ( t là số nguyên). Thay vào (1), ta được:
3x + 17.3t = 159
x + 17t = 53
=> x =53 - 17t
Do đó \(\hept{\begin{cases}x=53-17t\\y=3t\end{cases}}\left(t\in Z\right)\)
Đảo lại thay các biểu thức của x và y vào (1) được nghiệm đúng.
Vậy (1) có vô số (x; y) nguyên được biểu thị bởi công thức:
\(\hept{\begin{cases}x=53-17t\\y=3t\end{cases}}\left(t\in Z\right)\)
TN
7 tháng 6 2016
pt<=>17y=159-3x
<=>17y=3(53-x)
=>17y chia hết 3
mà (3,17)=1 =>y=3k (k thuộc Z)
=>x=53-17x
Vậy pt có dạng tổng quát:
x=53-17k;y=3k
Q
7
NK
2
6 tháng 2 2017
=> \(\frac{1}{53}\)+ \(\frac{-1}{106}\)+\(\frac{-1}{159}\)= \(\frac{\left|x\right|}{318}\)
=> \(\frac{1}{318}\)= \(\frac{\left|x\right|}{318}\)
=> x thuộc {1; -1}
AT
6 tháng 2 2017
\(\left(1-\frac{52}{53}\right)+\left(\frac{105}{106}-1\right)+\left(\frac{158}{159}-1\right)=\frac{\left|x\right|}{318}\)
\(\Rightarrow\frac{1}{53}+\frac{-1}{106}+\frac{-1}{159}=\frac{\left|x\right|}{318}\)
\(\Rightarrow\frac{1}{318}=\frac{\left|x\right|}{318}\)
\(\Rightarrow\left|x\right|=1\)
\(\Rightarrow x=\pm1\)
Vậy..............................
LL
6 tháng 12 2020
\(\left(1-\frac{52}{53}\right)+\left(\frac{105}{106}-1\right)+\left(\frac{158}{159}-1\right)=\frac{\left|x\right|}{318}\)
⇔\(\frac{1}{53}+\frac{-1}{106}+\frac{-1}{159}=\frac{\left|x\right|}{318}\)
⇔\(\frac{1}{138}=\frac{\left|x\right|}{318}\)
⇒\(\left|x\right|=1\)
⇔\(\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
Vậy x∈\(\left\{-1;1\right\}\)
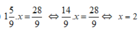
\(129-50x^2=-159\)
\(\Leftrightarrow50x^2=288\)
\(\Leftrightarrow x^2=\frac{144}{25}\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x=\frac{12}{5}\\x=-\frac{12}{5}\end{array}\right.\)
\(129-50x^2=-159\)
\(\Rightarrow50x^2=288\)
\(\Rightarrow x^2=\frac{144}{25}\)
\(\Rightarrow x=\frac{12}{5}\) hoặc \(x=\frac{-12}{5}\)
Vậy \(x=\frac{12}{5}\) hoặc \(x=\frac{-12}{5}\)