N
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
29 tháng 1 2022
Xét ΔDBC có
BA là đường trung tuyến
BA=DC/2
Do đó: ΔDCB vuông tại B
D
2
15 tháng 7 2021
Theo đề bài ta có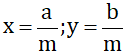 
(a, b, m ∈ Z; m > 0).
Quy đồng mẫu số các phân số ta được: 
Nhận xét: mẫu số 2m > 0 nên để so sánh x, y, z ta so sánh các tử số 2a, 2b, a+b.
Vì a < b nên a + a < b + a hay 2a < a + b.
Vì a < b nên a + b < b + b hay a + b < 2b.
Vậy ta có 2a < a+b < 2b nên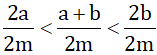 
hay x < z < y.
D
5
YN
23 tháng 2 2020
Hình tự vẽ
+) Xét \(\Delta\)DEF vuông tại D
\(\Rightarrow EF^2=ED^2+DF^2\) ( đl Py-ta-go)
\(\Rightarrow DE^2=EF^2-DF^2\)
\(\Rightarrow DE^2=10^2-6^2\)
\(\Rightarrow DE^2=100-36=64\)
\(\Rightarrow DE=\sqrt{64}=8\) (cm) ( do DE > 0 )
Vậy DE = 8 ( cm)
19 tháng 4 2017
a)Xét \(A\left(1\right)=a.1^2+b.1+c\)
\(\Rightarrow A\left(1\right)=a+b+c=0\)
Vậy \(x=1\) là một nghiệm của đa thức \(A\left(x\right)\)
b) Xét \(A\left(-1\right)=a.\left(-1\right)^2+b.\left(-1\right)+c\)
\(\Rightarrow A\left(-1\right)=a-b+c=0\)
Vậy \(x=-1\) là một nghiệm của đa thức \(A\left(x\right)\)
8 tháng 12 2017
Gọi số thanh rây dài 10m cần để làm đường sắt là x.
Ta có:
- Để làm 1 đoạn đường sắt phải dùng 960 thanh rây dài 8m.
- Để làm 1 đoạn đường sắt phải dùng x thanh rây dài 10m.
Vì số thanh rây và chiều dài của chúng là 2 đại lượng tỉ lệ nghịch.
Ta có : \(\dfrac{960}{x}=\dfrac{10}{8}\)⇒\(x=\dfrac{960.8}{10}=768\)
Vậy cần 768 thanh dây 10m để làm đoạn đường sắt đó.
12 tháng 3 2020
\(a,\left|2x-5\right|=1\)
\(\Rightarrow\orbr{\begin{cases}2x-5=1\\2x-5=-1\end{cases}\Rightarrow\orbr{\begin{cases}2x=6\\2x=4\end{cases}\Rightarrow}\orbr{\begin{cases}x=3\\x=2\end{cases}}}\)
b, đề thiếu
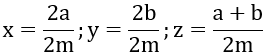
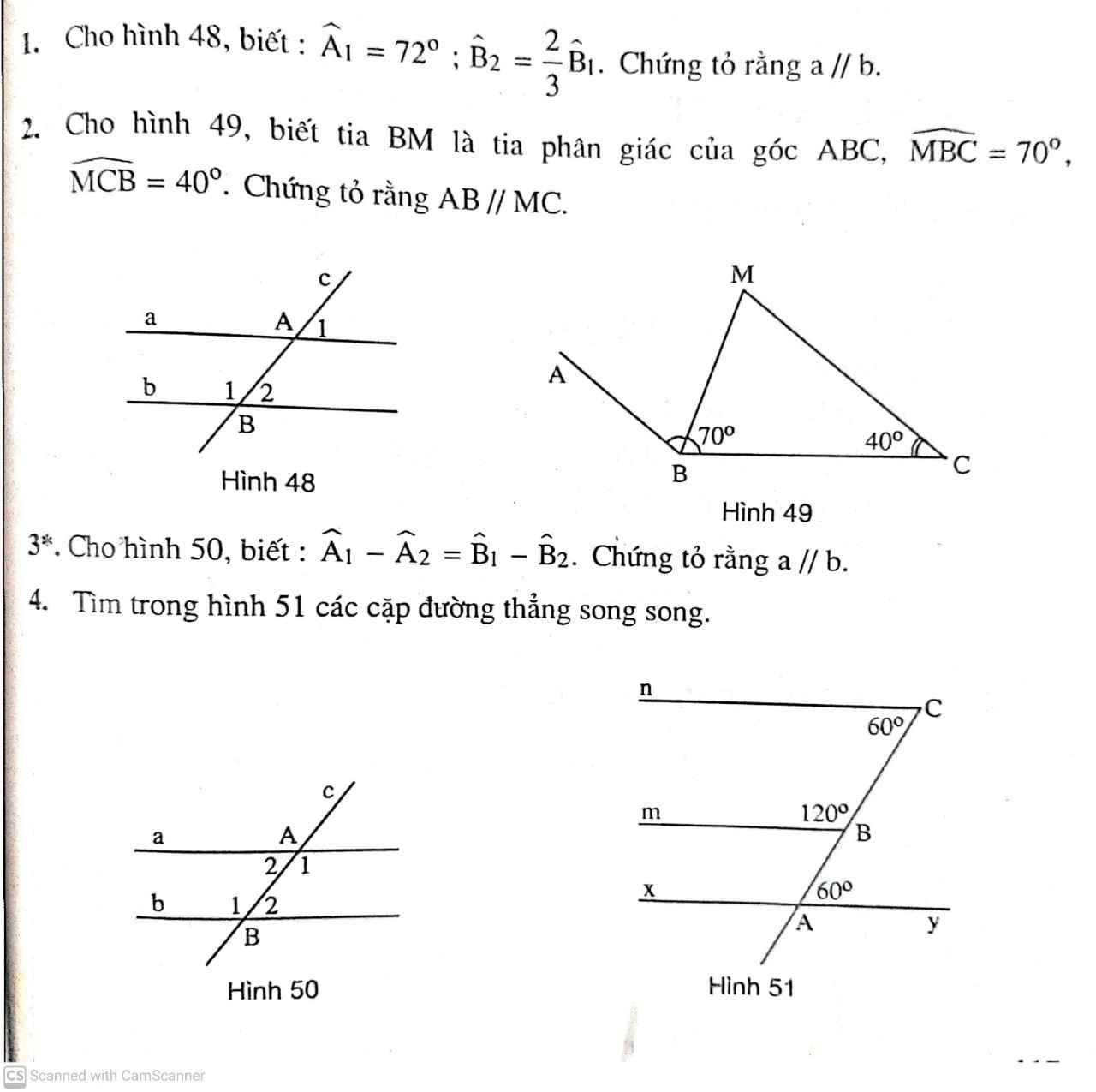
\(|2x-5|-|4x-7|=12\left(1\right)\)
Ta có:
\(2x-5=0\Leftrightarrow x=\frac{5}{2}\)
\(4x-7=0\Leftrightarrow x=\frac{7}{4}\)
Lập bảng xét dấu :
+) Với \(x< \frac{5}{2}\Rightarrow\hept{\begin{cases}2x-5< 0\\4x-7< 0\end{cases}\Rightarrow\hept{\begin{cases}|2x-5|=5-2x\\|4x-7|=7-4x\end{cases}\left(2\right)}}\)
Thay (2) vào (1) ta được :
\(\left(5-2x\right)-\left(7-4x\right)=12\)
\(5-2x-7+4x=12\)
\(-2+2x=12\)
\(2x=14\)
\(x=7\)( loại )
+) Với \(\frac{5}{2}\le x\le\frac{7}{4}\Rightarrow\hept{\begin{cases}2x-5>0\\4x-7< 0\end{cases}\Rightarrow\hept{\begin{cases}|2x-5|=2x-5\\|4x-7|=7-4x\end{cases}\left(3\right)}}\)
Thay (3) vào (1) ta được :
\(\left(2x-5\right)-\left(7-4x\right)=12\)
\(2x-5-7+4x=12\)
\(6x-12=12\)
\(6x=24\)
\(x=4\)(loại )
+) Với \(x>\frac{7}{4}\Rightarrow\hept{\begin{cases}2x-5>0\\4x-7>0\end{cases}\Rightarrow\hept{\begin{cases}|2x-5|=2x-5\\|4x-7|=4x-7\end{cases}\left(4\right)}}\)
Thay (4) vào (1) ta được :
\(\left(2x-5\right)-\left(4x-7\right)=12\)
\(2x-5-4x+7=12\)
\(-2x+2=12\)
\(-2x=10\)
\(x=-5\)(loại )
Vậy ko có giá trị x nào thỏa mãn đầu bài.
à sorry bài anh sai rồi để anh làm lại nhé