Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: f(-1)=-1
f(1/2)=-1/4
c: \(f\left(1\right)=-1^2=-1=y_E\)
Do đó: E thuộc đồ thị
\(f\left(-2\right)=-\left(-2\right)^2=-4< >y_F\)
Do đó: F không thuộc đồ thị
d: Thay x=-3 vào f(x), ta được:
\(f\left(-3\right)=-\left(-3\right)^2=-9\)

1: Để hàm số đồng biến thì m-3>0
hay m>3
2: Thay x=0 và y=0 vào (d), ta được:
3m+7=0
hay \(m=-\dfrac{7}{3}\)

\(a,\Leftrightarrow y=0;x=2\Leftrightarrow2m-2+m-2=0\Leftrightarrow m=\dfrac{4}{3}\)
\(b,\) PT giao Ox: \(\Leftrightarrow\left(m-1\right)x=2-m\Leftrightarrow x=\dfrac{2-m}{m-1}\Leftrightarrow A\left(\dfrac{2-m}{m-1};0\right)\Leftrightarrow OA=\left|\dfrac{2-m}{m-1}\right|\)
PT giao Oy: \(y=m-2\Leftrightarrow B\left(0;m-2\right)\Leftrightarrow OB=\left|m-2\right|\)
\(S_{OAB}=\dfrac{2}{3}\Leftrightarrow\dfrac{1}{2}OA\cdot OB=\dfrac{2}{3}\Leftrightarrow\left|\dfrac{2-m}{m-1}\cdot\left(m-2\right)\right|=\dfrac{4}{3}\\ \Leftrightarrow\left|\dfrac{-\left(m-2\right)^2}{m-1}\right|=\dfrac{4}{3}\Leftrightarrow\left[{}\begin{matrix}\dfrac{-\left(m-2\right)^2}{m-1}=\dfrac{4}{3}\left(1\right)\\\dfrac{-\left(m-2\right)^2}{1-m}=\dfrac{4}{3}\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow-3m^2+12m-12=4m-4\\ \Leftrightarrow3m^2-9m+9=0\\ \Leftrightarrow m\in\varnothing\\ \left(2\right)\Leftrightarrow-3m^2+12m-12=4-4m\\ \Leftrightarrow3m^2-16m+16=0\\ \Leftrightarrow\left[{}\begin{matrix}m=4\\m=\dfrac{4}{3}\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}m=4\\m=\dfrac{4}{3}\end{matrix}\right.\) thỏa đề
\(c,\) Gọi \(E\left(x_0;y_0\right)\) là điểm cần tìm
\(\Leftrightarrow\left(m-1\right)x_0+m-2=y_0\\ \Leftrightarrow mx_0+m-x_0-y_0-2=0\\ \Leftrightarrow m\left(x_o+1\right)-\left(x_0+y_0+2\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_0=-1\\y_0=-2-x_0=-1\end{matrix}\right.\Leftrightarrow E\left(-1;-1\right)\)

\(S=\dfrac{3}{1.4}+\dfrac{3}{4.7}+...+\dfrac{3}{43.46}\\ =1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{43}-\dfrac{1}{46}\\ =1-\dfrac{1}{46}\\ =\dfrac{45}{46}\\ \Rightarrow S< 1\)

a) Bảng giá trị:

Đồ thị:
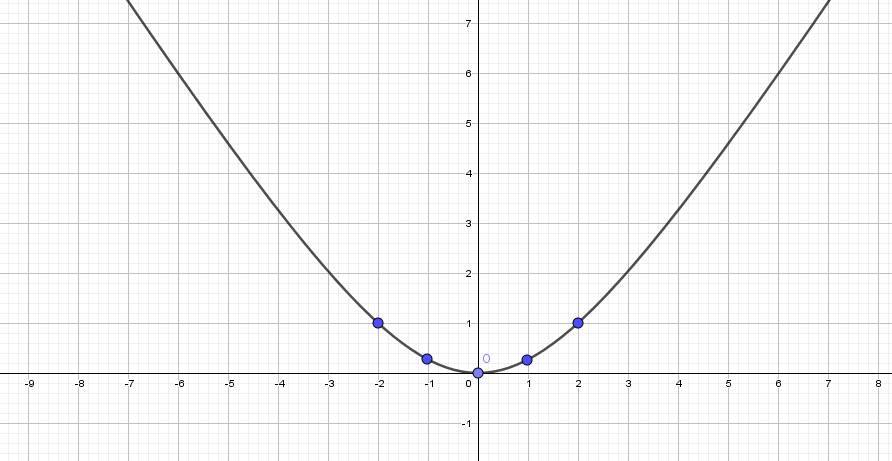
b) Thay y = 100 vào (P) ta được:
\(\dfrac{1}{4}x^2=100\)
\(\Leftrightarrow x^2=100:\dfrac{1}{4}\)
\(\Leftrightarrow x^2=400\)
\(\Leftrightarrow\left[{}\begin{matrix}x=20\\x=-20\end{matrix}\right.\)
Vậy M(-20; 100) hoặc M(20; 100)