
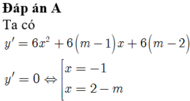
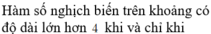
![]()

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

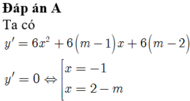
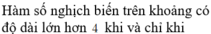
![]()


Theo mình:
để hàm số đồng biến, đk cần là y'=0.
a>0 và \(\Delta'< 0\)
nghịch biến thì a<0
vì denta<0 thì hầm số cùng dấu với a
mình giải được câu a với b
câu c có hai cực trị thì a\(\ne\)0, y'=0, denta>0 (để hàm số có hai nghiệm pb)
câu d dùng viet
câu e mình chưa chắc lắm ^^

\(y'=-x^2-2\left(m-2\right)x+m-2\)
Hàm nghịch biến trên TXĐ khi và chỉ khi \(y'\le0;\forall x\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=-1< 0\left(đúng\right)\\\Delta'=\left(m-2\right)^2+m-2\le0\end{matrix}\right.\)
\(\Leftrightarrow\left(m-2\right)\left(m-1\right)\le0\)
\(\Leftrightarrow1\le m\le2\)

Đáp án B
Phương pháp:
Hàm số y = f(x) nghịch biến trên (-∞;+∞) khi và chỉ khi f'(x) ≤ 0, ∀ x ∈ (-∞;+∞), f'(x) = 0 tại hữu hạn điểm.
Cách giải:
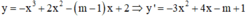
Hàm số đã cho nghịch biến trên khoảng (-∞;+∞)
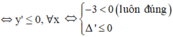
![]()
![]()
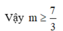

3.
\(y'=\dfrac{3m-1}{\left(x+3m\right)^2}\)
Hàm nghịch biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-1< 0\\-3m\le6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< \dfrac{1}{3}\\m\ge-2\end{matrix}\right.\)
\(\Rightarrow-2\le m< \dfrac{1}{3}\Rightarrow m=\left\{-2;-1;0\right\}\)
4.
\(y'=\dfrac{3m-2}{\left(x+3m\right)^2}\)
Hàm đồng biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-2>0\\-3m\ge-6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>\dfrac{2}{3}\\m\le2\end{matrix}\right.\)
\(\Rightarrow\dfrac{2}{3}< m\le2\Rightarrow m=\left\{1;2\right\}\)

Đáp án: A.
Hàm số nghịch biến trên từng khoảng ( - ∞ ; -m), (-m; + ∞ ) khi và chỉ khi
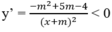
⇔ - m 2 + 5m - 4 < 0
⇔ 

Đáp án: A.
Hàm số nghịch biến trên từng khoảng (- ∞ ; -m), (-m; + ∞ ) khi và chỉ khi
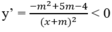
⇔ - m 2 + 5m - 4 < 0
⇔ ![]()