Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Bất phương trình
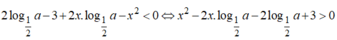
Đặt , 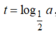 khi đó bất phương trình trở thành x2-2tx-2t+3> 0 (*)
khi đó bất phương trình trở thành x2-2tx-2t+3> 0 (*)
Bất phương trình (*) nghiệm đúng với mọi x khi và chỉ khi
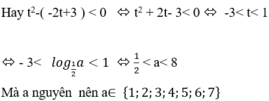
Vậy có tất cả 7 giá trị nguyên của a thỏa mãn yêu cầu bài toán.

\(\left(3^x-27\right)\left(x^2-x-20\right)\ge0\Leftrightarrow\left[{}\begin{matrix}-4\le x\le3\\x\ge5\end{matrix}\right.\)
\(\Rightarrow\) Có \(8+40-5+1=44\) nghiệm nguyên

Đáp án D.
Đặt t = log3 x => t2 – 3t + 2m – 7 = 0
PT có 2 nghiệm khi ∆ = 9 - 4 2 m - 7 = 37 - 8 m > 0
=> PT có 2 nghiệm t1; t2
⇒ log 3 x 1 = t 1 log 3 x 2 = t 2 ⇒ x 1 = 3 t 1 x 2 = 3 t 2
Khi đó theo định lý Viet ta có:
t 1 + t 2 = 3 t 1 . t 2 = 2 m - 7
Do

Đặt
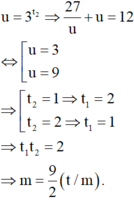

Đáp án B.
Đặt t = log2 x,
khi đó m + 1 log 2 2 x + 2 log 2 x + m - 2 = 0
⇔ m + 1 t 2 + 2 t + m - 2 = 0 (*).
Để phương trình (*) có hai nghiệm phân biệt
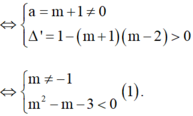
Khi đó gọi x1, x2 lần lượt hai nghiệm của phương trình (*).
Vì 0 < x1 < 1 < x2 suy ra
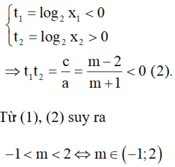

Đáp án B
Điều kiện
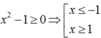
Phương trình đã cho tương đương với:
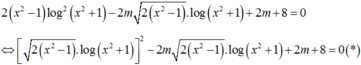
Đặt t = x 2 ≥ 1 , theo bài ra ta có 1 ≤ x 1 < x 2 ≤ 3 ⇔ 1 ≤ x 1 2 < x 2 2 ≤ 9 ⇒ t ∈ 1 ; 9
Xét hàm số f ( t ) = 2 - ( t - 1 ) . log ( t + 1 ) trên đoạn 1 ; 9 .
Ta có
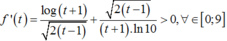
⇒ Hàm số f ( t ) đồng biến trên đoạn 1 ; 9 . Khi đó f ( 1 ) ≤ f ( t ) ≤ 9 hay 1 ≤ f ( t ) ≤ 4 .
Đặt u = 2 ( x 2 - 1 ) . log ( x 2 + 1 ) ⇒ u ∈ 0 ; 4 . Khi đó phương trình * trở thành u 2 - 2 m . u + 2 m + 8 = 0 1 .
Nhận thấy u = 1 không phải là nghiệm của phương trình 1 . Với u ≠ 1 thì phương trình 1 tương đương với u 2 + 8 = 2 m ( u - 1 ) ⇔ 2 m = u 2 + 8 u - 1 2
Xét hàm số g u = u 2 + 8 u - 1 trên đoạn 0 ; 4 \ 1 .
Ta có g ' u = u 2 - 2 u - 8 u - 1 2 ; g ' ( u ) = 0 ⇔ [ u = - 2 u = 4 . Mà u ∈ 0 ; 4 \ 1 nên u = 4 .
Mặt khác, có g ( 0 ) = - 8 ; g ( 4 ) = 8 ; lim x → 1 - g ( u ) = - ∞ ; lim x → 1 + g ( u ) = = ∞ .
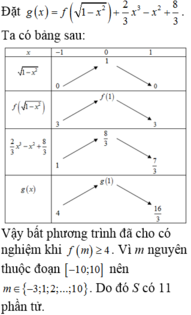
Bảng biến thiên:
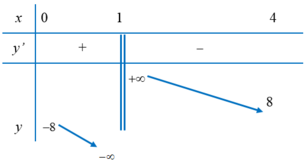
Yêu cầu bài toán ⇔ Phương trình 2 có nghiệm duy nhất trên đoạn 0 ; 4 \ 1 .
Suy ra
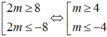
Mặt khác m ∈ ℤ , m ∈ - 2017 ; 2017 nên suy ra
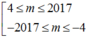
Vậy có tất cả 2017 - 4 + 1 + - 4 + 2017 + 1 = 4028 giá trị m nguyên thỏa mãn bài toán.


a= {0;6;12}
a={-42;-14;-8;0;6;12}