Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Với \(m=0\) ko thỏa mãn
Với \(m\ne0\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{x+1}{\sqrt{mx^2+1}}=-\dfrac{1}{\sqrt{m}}\); \(\lim\limits_{x\rightarrow+\infty}\dfrac{x+1}{\sqrt{mx^2+1}}=\dfrac{1}{\sqrt{m}}\)
\(\Rightarrow\) Hàm có 2 TCN khi \(\sqrt{m}\) xác định \(\Rightarrow m>0\)

Ta có
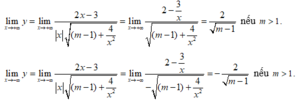
Vậy với m > 1 thì đồ thị hàm số 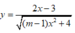 có hai tiệm cận ngang là
có hai tiệm cận ngang là 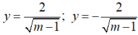
Chọn đáp án C.

ĐKXĐ: \(x\le1\)
Hàm có tiệm cận đứng khi và chỉ khi phương trình:
\(x-m=0\) có nghiệm \(x< 1\)
\(\Leftrightarrow m< 1\)

Do mẫu có bậc 2 còn tử bậc 1 \(\Rightarrow\)hàm không có tiệm cận đứng khi và chỉ khi phương trình \(x^2-2mx+1=0\) vô nghiệm
\(\Leftrightarrow\Delta'=m^2-1< 0\)
\(\Rightarrow-1< m< 1\)

Điều kiện: x ≤ 1 x ≠ m
-Nếu m> 1 thì lim x → m + y ; lim x → m - y không tồn tại nên đồ thị hàm số không có tiệm cận đứng.
Nếu m= 1 thì hàm số trở thành y = 1 - x x - 1
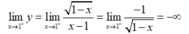
Suy ra đường thẳng x= 1 là tiệm cận đứng của đồ thị hàm số khi x → 1 - .
lim x → 1 + y không tồn tại.
Do đó, m= 1 thỏa mãn.
- Nếu m< 1 thì
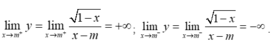
Suy ra đường thẳng x= m là tiệm cận đứng của đồ thị hàm số khi x → m + v à x → m -
Vậy m ≤ 1 thỏa mãn yêu cầu đề bài.
Chọn C.

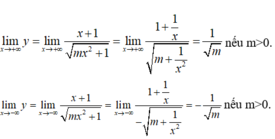


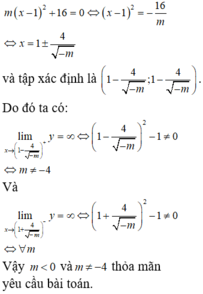
Điều kiện:mx2+1>0.
- Nếu m=0 thì hàm số trở thành y=x+1 không có tiệm cận ngang.
- Nếu m<0 thì hàm số xác định ⇔ - 1 - m < x < 1 - m
Do đó, lim x → ± ∞ y không tồn tại nên đồ thị hàm số không có tiệm cận ngang.
- Nếu m>0 hì hàm số xác định với mọi x.
Suy ra đường thẳng y = 1 m là tiệm cận ngang của đồ thị hàm số khi x → + ∞ .
Suy ra đường thẳng y = - 1 m là tiệm cận ngang của đồ thị hàm số.
Vậy m>0 thỏa mãn yêu cầu đề bài.
Chọn B.