Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có \(f\left(x\right)>0,\forall x\in\left(0;1\right)\)
\(\Leftrightarrow-x^2-2\left(m-1\right)x+2m-1>0,\forall x\left(0;1\right)\)
\(\Leftrightarrow-2m\left(x-1\right)>x^2-2x+1,\forall x\in\left(0;1\right)\) (*)
Vì \(x\in\left(0;1\right)\Rightarrow x-1< 0\) nên (*) \(\Leftrightarrow-2m< \dfrac{x^2-2x+1}{x-1}=x-1=g\left(x\right),\forall x\in\left(0;1\right)\)
\(\Leftrightarrow-2m\le g\left(0\right)=-1\Leftrightarrow m\ge\dfrac{1}{2}\)

`@TH1: m-1=0<=>m=1`
`=>2x+1 > 0<=>x > -1/2`
`=>m=1` loại
`@TH2: m-1 ne 0<=>m ne 1`
`=>(m-1)x^2-2(m-2)x+2-m > 0 AA x in RR`
`=>{(m-1 > 0),(\Delta' < 0):}`
`<=>{(m > 1),((m-2)^2-(2-m)(m-1) < 0):}`
`<=>{(m > 1),(3/2 < m < 2):}`
`=>3/2 < m < 2`

Để hàm số xác định thì x-m+2>=0 và x-m+2<>1
=>x>=m-2 và x<>m-1
=>m-2<=0 và \(m-1\notin\left(0;1\right)\)
=>m<=2 và (m-1<=0 hoặc m-1>=1)
=>m=2 hoặc m<=1

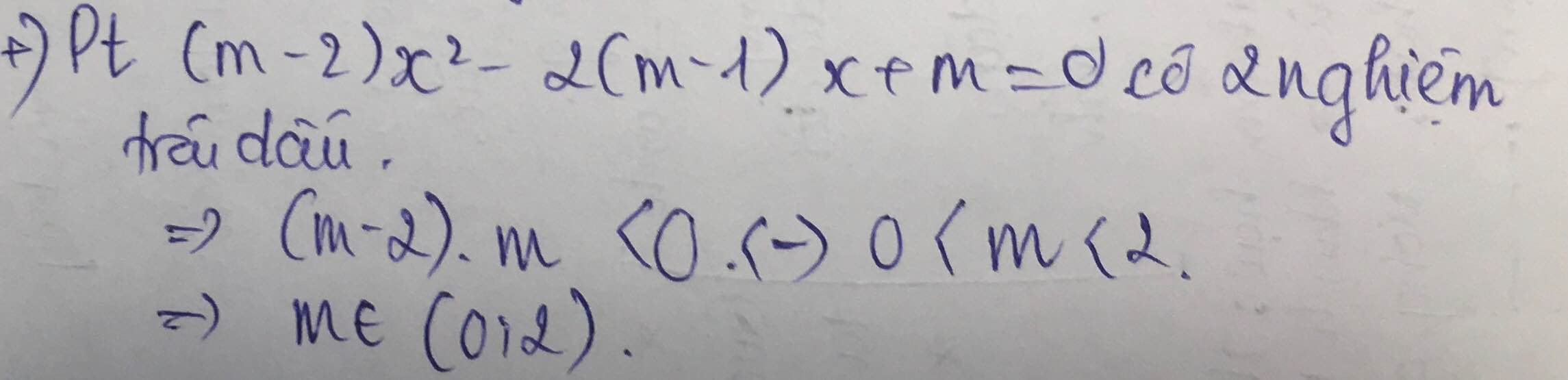


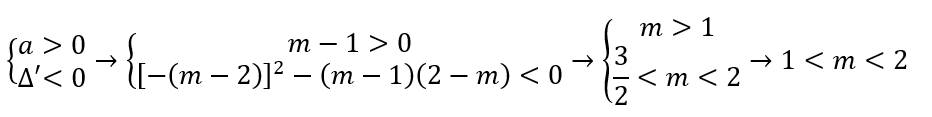

Đáp án C