Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tích phân đã cho tồn tại khi hàm \(\dfrac{1}{x\left(x-5\right)\left(x-4\right)}\) xác định với mọi x thuộc \(\left[1;1+a\right]\) với \(a>0\) hoặc \(\left[1+a;1\right]\) với \(a< 0\)
ĐKXĐ: \(x\ne\left\{0;4;5\right\}\) hay \(x\in\left(-\infty;0\right)\cup\left(0;4\right)\cup\left(4;5\right)\cup\left(5;+\infty\right)\)
Do 2 khoảng \(\left[1;1+a\right]\) và \(\left[1+a;1\right]\) đều chứa số 1 nằm trong \(\left(0;4\right)\)
\(\Rightarrow\)Bài toán thỏa mãn khi \(\left[{}\begin{matrix}\left[1;a+1\right]\subset\left(0;4\right)\\\left[1+a;1\right]\subset\left(0;4\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}1< 1+a< 4\\0< 1+a< 1\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}0< a< 3\\-1< a< 0\end{matrix}\right.\)

Ta có:
\(y'=x^2-2mx+m^2-4\)
\(y''=2x-2m,\forall x\in R\)
Để hàm số \(y=\dfrac{1}{3}x^3-mx^2+\left(m^2-4\right)x+3\) đạt cực đại tại x = 3 thì:
\(\left\{{}\begin{matrix}y'\left(3\right)=0\\y''\left(3\right)< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2-6m+5=0\\6-2m< 0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m=1,m=5\\m>3\end{matrix}\right.\Leftrightarrow m=5\)
=> B.

Xét phương trình hoành độ giao điểm:
2 x + 1 x + 1 = x + m - 1 ( x ≠ - 1 ) ⇔ x 2 + ( m - 2 ) x + ( m - 2 ) = 0 ( * )
Đường thẳng d cắt (C) tại hai điểm phân biệt khi và chỉ khi phương trình có hai nghiệm phân biệt khác - 1
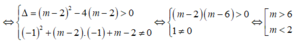
Khi đó d cắt ( C) tại A( x1; x1+ m- 1) ; B ( x2; x2+ m- 1)
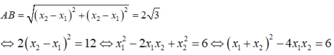
Áp dụng định lý Vi-et x 1 + x 2 = - m + 2 x 1 x 2 = m - 2 ta có:
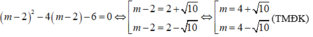
Vậy m = 4 ± 10
Chọn B.

\(f'\left(x\right)=m^2x^4-mx^2+20x-\left(m^2-m-20\right)\)
Để hàm số đồng biến trên \(ℝ\)thì \(f'\left(x\right)\ge0,\)với mọi \(x\inℝ\).
Mà ta thấy \(f'\left(-1\right)=m^2-m-20-\left(m^2-m-20\right)=0\)
do đó \(x=-1\)là một điểm cực trị của hàm số \(f'\left(x\right)\).
Ta có: \(f''\left(x\right)=4m^2x^3-2mx+20\)
\(f''\left(-1\right)=0\Leftrightarrow-4m^2+2m+20=0\Leftrightarrow\orbr{\begin{cases}m=\frac{5}{2}\\m=-2\end{cases}}\).
Thử lại.
Với \(m=\frac{5}{2}\): \(f''\left(x\right)=25x^3-5x+20\)
\(f''\left(x\right)=0\Leftrightarrow x=-1\)
\(f'\left(-1\right)=0\)
do đó \(f'\left(x\right)\ge0\)thỏa mãn.
Với \(m=-2\): \(f''\left(x\right)=16x^3+4x+20\)
\(f''\left(x\right)=0\Leftrightarrow x=-1\).
\(f'\left(-1\right)=0\)
do đó \(f'\left(x\right)\ge0\)thỏa mãn.
Vậy tổng các giá trị của \(m\)là: \(\frac{5}{2}+\left(-2\right)=\frac{1}{2}\).
Chọn D.


Đáp án A