Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Đặt ![]()
Khi đó, phương trình f(
4
x
-
x
2
) =
log
2
m
trở thành ![]()
Để phương trình f( 4 x - x 2 ) = log 2 m có 4 nghiệm thực phân biệt thì đường thẳng y = log 2 m cắt đồ thị hàm số y = f(t) tại hai điểm phân biệt thỏa mãn t < 4.
Suy ra ![]()
Vậy m ∈ ( 1 2 ;8).

Đáp án D
Ta có log0,02[log2 (3x + 1)] > log0,02 m
<=> m > log2 (3x + 1) (vì cơ số = 0,02 < 1)
Xét hàm số f(x) = log2 (3x + 1) trên - ∞ ; 0
có f ' x = 3 x . ln 3 3 x + 1 ln 2 > 0 ; ∀ x ∈ - ∞ ; 0
Suy ra f(x) là hàm số đồng biến trên - ∞ ; 0
⇒ m a x - ∞ ; 0 f x = f 0 = 1
Vậy để bất phương trình có nghiệm ∀ x ∈ - ∞ ; 0 ⇒ m ≥ 1 .

Đáp án A
Phương pháp:
Cô lập m, đưa về dạng f(x) = m
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = m
Cách giải:
Điều kiện: x ≠ 2, x ≠ -4
![]()
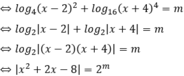
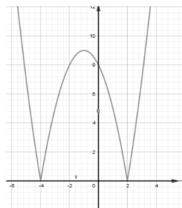
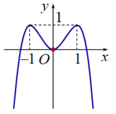
Số nghiệm của phương trình đã cho bằng số giao điểm của đồ thị hàm số y = |x2 + 2x - 8| và đường thẳng y = 2m
Quan sát đồ thị hàm số bên, ta thấy, để đồ thị hàm số y = |x2 + 2x - 8| cắt đường thẳng y = 2m tại 4 điểm phân biệt thì 0 < 2m < 9 ⇔ m < log29 ⇔ m < 2 log23

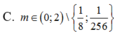
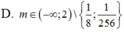
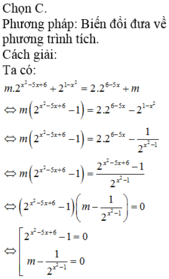

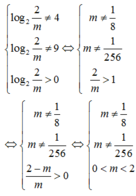


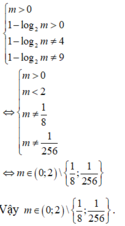


Chọn C.