Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có y ' = 3 ( m - 1 ) + ( 2 m + 1 ) sin x để hàm số nghịch biến trên ℝ thì y ' ≤ 0 với mọi x xét BPT
3 ( m - 1 ) + ( 2 m + 1 ) sin x ≤ 0 Nếu m = - 1 2 BPT luôn đúng. Với m > - 1 2 BPT ⇔ sin x ≤ 3 ( 1 - m ) 2 m + 1 để hàm số luôn nghịch biến với mọi x thì 3 ( 1 - m ) 2 m + 1 ≥ 1 ⇒ - 1 2 < m ≤ 2 5 . Với m < - 1 2 BPT ⇔ sin x ≥ 3 ( 1 - m ) 2 m + 1 để hàm số luôn nghịch biến với mọi x thì 3 ( 1 - m ) 2 m + 1 ≤ - 1 ⇒ m < - 1 2
Kết hợp hai trường hợp ta có m ≤ 2 5

Đáp án B
Để ý thấy lời giải bài toán sai ở bước 3 do m có thể nhỏ hơn 0

Từ giả thiết, thay x bởi x-1 ta được ![]()
Khi đó ta có 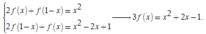
Suy ra ![]()
YCBT ![]()
![]()
Chọn B.

Đáp án C

Bảng biến thiên của hàm số f(x) là
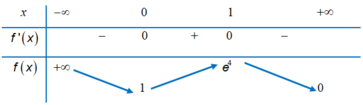
Hàm số f x là hàm số chẵn trên ℝ nên đồ thị của hàm số nhận trục tung làm trục đối xứng. Do đó phương trình f ( x ) + m = 0 có bốn nghiệm thực phân biệt khi và chỉ khi phương trình f ( x ) + m = 0 có hai nghiệm dương phân biệt hay phương trình f ( x ) = - m có hai nghiệm dương phân biệt
⇔ 1 < - m < e 4 ⇔ - e 4 < m < - 1


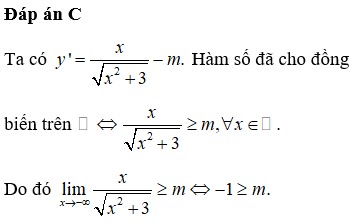
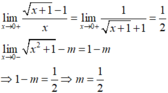
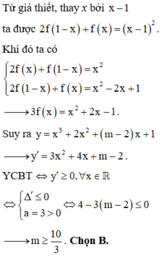
Đáp án là B.
Ta có y ' ( x ) = ( m - 1 ) x 2 - 2 ( m - 1 ) x - 1
TH1. m - 1 = 0 ⇔ m = 1 .Khi đó
y , = - 1 < 0 , ∀ x ∈ ℝ .Nên hàm só luôn nghịch biếến trên ℝ .
TH2. m - 1 ≢ 0 ⇔ m ≢ 1 .Hàm số luôn nghịch biến trên ℝ khi
y , ≤ 0 , ∀ x ∈ ℝ ⇔ ( m - 1 ) x 2 - 2 ( m - 1 ) x - 1 ≤ 0 , ∀ x ∈ ℝ ⇔ m - 1 < 0 ∆ ' ≤ 0 ⇔ m < 1 m ( m - 1 ) ≤ 0 ⇔ 0 ≤ m ≤ 1 . Kết hợp ta được 0 ≤ m < 1 .