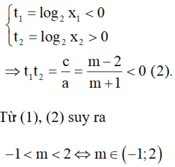Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án: D.
Xét hàm số
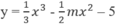
Ta có: y' = x 2 - mx = 0 ⇔ x = 0 hoặc x = 3
Nếu m = 0: Phương trình thành x 3 /3 - 5 = 0, có nghiệm duy nhất.
Nếu m ≠ 0: Phương trình đã cho có nghiệm duy nhất khi và chỉ khi cực đại và cực tiểu của hàm số
![]()
cùng dấu.
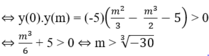

Đáp án: B.
Với m = 0, phương trình 2 x 3 - 5 = 0 có nghiệm duy nhất.
Với m ≠ 0, đồ thị hàm số y = 2 x 3 + 3m x 2 - 5 chỉ cắt Ox tại một điểm khi y CĐ . y CT > 0. Ta có y' = 6 x 2 + 6mx = 6x(x + m) = 0 có hai nghiệm là x = 0, x = -m; y(0) = -5, y(-m) = -2 m 3 + 3 m 3 - 5 = m 3 - 5.
Suy ra y(0).y(-m) = -5( m 3 - 5) > 0 ⇔ m < 5 3

\(f^2\left(\left|x\right|\right)-\left(m-6\right)f\left(\left|x\right|\right)-m+5=0\) có \(a-b+c=0\) nên có các nghiệm \(\left[{}\begin{matrix}f\left(\left|x\right|\right)=-1\\f\left(\left|x\right|\right)=m-5\end{matrix}\right.\)
- Với \(f\left(\left|x\right|\right)=-1\Rightarrow\left|x\right|^2-4\left|x\right|+3=-1\Rightarrow\left|x\right|=2\Rightarrow x=\pm2\) có 2 nghiệm
- Xét \(f\left(\left|x\right|\right)=m-5\Leftrightarrow\left|x\right|^2-4\left|x\right|+8=m\) (1)
Từ BBT của \(y=\left|x\right|^2-4\left|x\right|+8\) dễ dàng suy ra (1) có 4 nghiệm pb khi \(4< m< 8\)
\(\Rightarrow m=\left\{5;6;7\right\}\) có 3 giá trị nguyên

Chọn D.
Đặt t = 3x > 0, phương trình trở thành t2 - (m - 1) t + 2m = 0 (*)
Yêu cầu bài toán thành phương trình (*) có đúng một nghiệm dương.
+ (*) có nghiệm kép dương 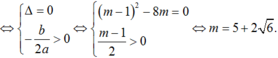
+ (*) có hai nghiệm trái dấu khi đó; 2m < 0 hay m < 0.
Vậy m < 0 hoặc ![]() thỏa yêu cầu bài toán.
thỏa yêu cầu bài toán.

Đáp án B.
Đặt t = log2 x,
khi đó m + 1 log 2 2 x + 2 log 2 x + m - 2 = 0
⇔ m + 1 t 2 + 2 t + m - 2 = 0 (*).
Để phương trình (*) có hai nghiệm phân biệt
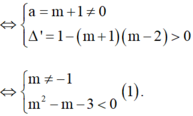
Khi đó gọi x1, x2 lần lượt hai nghiệm của phương trình (*).
Vì 0 < x1 < 1 < x2 suy ra