Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

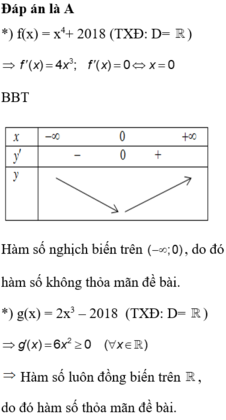
Đáp án là A
![]() nên hàm số có khoảng đồng biến và nghịch biến.
nên hàm số có khoảng đồng biến và nghịch biến.
![]() nên hàm số luôn đồng biến trên R.
nên hàm số luôn đồng biến trên R.
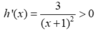 nên hàm số luôn đồng biến trên từng khoảng xác định.
nên hàm số luôn đồng biến trên từng khoảng xác định.
Vậy có 2 hàm số không có khoảng nghịch biến.

Ta có ![]() .
.
Hàm số nghịch biến trên khoảng ![]() khi và chỉ khi
khi và chỉ khi ![]() với
với ![]() hay
hay ![]() với
với ![]() .
.
Xét ![]() trên khoảng
trên khoảng ![]() ta có
ta có
![]() ;
;
![]() .
.
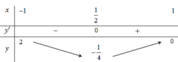
Bảng biến thiên
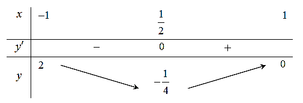
Dựa vào bảng biến thiên ta có ![]() với
với ![]()
![]() .
.
Đáp án A

Chọn B.
Với ![]() ,
,
xét từng TH phá dấu trị tuyệt đối, ta tìm được nghiệm
-3 ≤ y ≤ 0
Khi đó 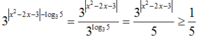 và
và ![]()
Do đó
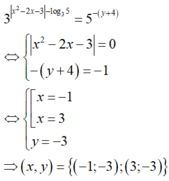
Vậy có tất cả hai cặp số thực (x; y) thỏa mãn yêu cầu bài toán.

Tập xác định: D= R\ { 2; 3}
lim x → 2 + 2 x - 1 - x 2 + x + 3 x 2 - 5 x + 6 = lim x → 2 + ( 2 x - 1 ) 2 - ( x 2 + x + 3 ) ( x 2 - 5 x + 6 ) ( 2 x - 1 + x 2 + x + 3 ) = lim x → 2 + 3 x + 1 ( x - 3 ) ( 2 x - 1 + x 2 + x + 3 ) = - 7 6
Tương tự lim x → 2 - 2 x - 1 - x 2 + x + 3 x 2 - 5 x + 6 = - 7 6 .
Suy ra đường thẳng x= 2 không là tiệm cận đứng của đồ thị hàm số đã cho.
lim x → 3 + 2 x - 1 - x 2 + x + 3 x 2 - 5 x + 6 = + ∞ ; lim x → 3 - 2 x - 1 - x 2 + x + 3 x 2 - 5 x + 6 = - ∞
Suy ra đường thẳng x= 3 là tiệm cận đứng của đồ thị hàm số đã cho.
Chọn D.

Đáp án B.
Với 4 y - y - 1 + y + 3 2 ≤ 8
xét từng TH phá giá trị tuyệt đối, ta tìm được nghiệm - 3 ≤ y ≤ 0
Khi đó 3 x 2 - 2 x - 3 - log 3 5 = 3 x 2 - 2 x - 3 3 log 3 5 = 3 x 2 - 2 x - 3 5 ≥ 1 5
và y ∈ - 3 ; 0 ⇔ y + 4 ∈ 1 ; 4 ⇒ 5 - y + 4 ≤ 5 - 1 = 1 5
Do đó
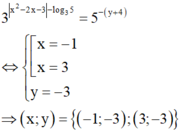
Vậy có tất cả hai cặp số thực (x; y) thỏa mãn yêu cầu bài toán.
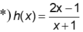

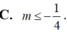
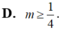

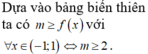


Đặt d : deg P(x) , ta có:
\(4=d^2\Leftrightarrow d=2\)
\(\Rightarrow P\left(x\right)=ax^2+bx+c\left(a\ne0\right)\)
Trog đó , hệ số cao nhất của vế trái là 1 nên a=1 . thay vào và thu gọn 2 vế đc:
\(x^4+2x^3+6x^2-8x+8=x^4+bx^3+\left(4+c\right).x^2+4bx+4c\)
Tiến hành đồng nhất, ta được:
\(\left\{{}\begin{matrix}b=-2\\c=2\end{matrix}\right.\)
suy ra: \(P\left(x\right)=x^2-2x+2\)
Đặt d : deg P(x) , ta có:
4=d2⇔d=24=d2⇔d=2
⇒P(x)=ax2+bx+c(a≠0)⇒P(x)=ax2+bx+c(a≠0)
Trong đó , hệ số cao nhất của vế trái là 1 nên a=1 . thay vào và thu gọn 2 vế đc:
x^4+2x^3+6x^2−8x+8=x^4+bx^3(4+c).x^2+4bx+4c
Tiến hành đồng nhất, ta được:
suy ra: P(x)=x^2−2x+2
mình chỉ bít zậy ko biết có đúng không nữa