LK
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LK
3
31 tháng 1 2020
Cái này nãy tui mới làm ở bên h_ọ_c_24 ý.
\(x\left(x-1\right)^2\ge4-x\)
\(\Leftrightarrow x\left(x^2-2x+1\right)\ge4-x\)
\(\Leftrightarrow x^3-2x^2+x\ge4-x\)
\(\Leftrightarrow x^3-2x^2+2x-4\ge0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2+2\right)\ge0\)
\(\Leftrightarrow x-2\ge0\left(Vì:x^2+2>0\forall x\right)\)
\(\Leftrightarrow x\ge2\)
Vậy \(S=\left\{2;+\infty\right\}\)
1 tháng 2 2020
@ Băng Băng @ Mình không kí hiệu tập nghiệm như vậy nhé em:
S = [ 2; \(+\infty\))
24 tháng 2 2022
2: \(\text{Δ}=1^2-4\cdot\left(-1\right)\cdot\left(-m\right)=1-4m\)
Để bất phương trình vô nghiệm thì \(\left\{{}\begin{matrix}1-4m< 0\\-1< 0\end{matrix}\right.\Leftrightarrow m>\dfrac{1}{4}\)
6 tháng 4 2020
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
7 tháng 4 2020
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 3 2022
\(\dfrac{x^2+x+3}{x^2-4}\ge1\Leftrightarrow\dfrac{x^2+x+3}{x^2-4}-1\ge0\)
\(\Leftrightarrow\dfrac{x+7}{x^2-4}\ge0\Rightarrow\left[{}\begin{matrix}-7\le x< -2\\x>2\end{matrix}\right.\)
\(\Rightarrow S\cap\left(-2;2\right)=\varnothing\)
LA
0
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 7 2021
- Với \(m=\dfrac{1}{2}\Rightarrow\left(x+1\right)^2>0\) có tập nghiệm \(R\backslash\left\{-1\right\}\) thỏa mãn
- Với \(m>\dfrac{1}{2}\) BPT có nghiệm: \(\left\{{}\begin{matrix}x>-1\\x< -2m\end{matrix}\right.\) hay \(D=\left(-\infty;-2m\right)\cup\left(-1;+\infty\right)\)
Thỏa mãn do \(\left(1;+\infty\right)\subset\left(-1;+\infty\right)\)
- Với \(m< \dfrac{1}{2}\) BPT có nghiệm: \(\left\{{}\begin{matrix}x>-2m\\x< -1\end{matrix}\right.\) hay \(D=\left(-\infty;-1\right)\cup\left(-2m;+\infty\right)\)
Tập nghiệm của BPT chứa \(\left(1;+\infty\right)\) khi:
\(-2m\le1\Rightarrow m\ge-\dfrac{1}{2}\Rightarrow-\dfrac{1}{2}\le m< \dfrac{1}{2}\)
Kết hợp lại ta được: \(m\ge-\dfrac{1}{2}\)
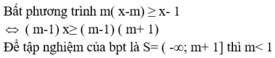
\(x\left(x-1\right)^2\ge4-x\)
\(\Leftrightarrow x\left(x^2-2x+1\right)\ge4-x\)
\(\Leftrightarrow x^3-2x^2+x\ge4-x\)
\(\Leftrightarrow x^3-2x^2+2x-4\ge0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2+2\right)\ge0\)
\(\Leftrightarrow x-2\ge\left(Vì:x^2+2>0\forall x\right)\)
\(\Leftrightarrow x\ge2\)
\(\Rightarrow S=\left\{2;+\infty\right\}\)
Sửa giúp mình nha. Dòng cuối á tại mới được cô Nguyễn Linh Chi bên olm nhắc =))
\(\Rightarrow S=[2;+\infty)\)