LQ
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TN
2
26 tháng 8 2017
các bạn nêu cách làm cụ thể giúp mình nha mình sẽ k cho
B
26 tháng 8 2017
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
26 tháng 3 2020
\(a,12⋮x-1\)
\(x-1\inƯ\left(12\right)=\left\{\pm1;\pm2;\pm3;\pm4;\pm12\right\}\)
Ta lập bảng xét giá trị
x - 1 1 -1 2 -2 3 -3 4 -4 12 -12
x 2 0 3 -1 4 -2 5 -3 13 -11
\(c,x+15⋮x+3\)
\(x+3+12⋮x+3\)
\(12⋮x+3\)
Tự lập bảng , lười ~~~
\(d,\left(x+1\right)\left(y-1\right)=3\)
Ta lập bảng
| x+1 | 1 | -1 | 3 | -3 |
| y-1 | 3 | -3 | 1 | -1 |
| x | 2 | 0 | 2 | -4 |
| y | 4 | -2 | 2 | 0 |
i, Theo bài ra ta có : ( olm thiếu dấu và == nên trình bày kiủ nài )
\(x⋮10,x⋮12,x⋮15\)và \(100< x< 150\)
Gợi ý : Phân tích thừa số nguyên tố r xét ''BC'' ( chắc là BC )
:>> Hc tốt
CD
1
CM
3 tháng 12 2018
a, Ta có: 42 = 2.3.7 = 1.42 = 2.21 = 3.14 = 6.7
Vì a < b nên ta tìm được các cặp số (a ;b) là (1;42), (2;21), (3;14), (6;7)
b, Ta có: 102 = 2.3.17 = 2.51 = 3.34 = 6.17
Vì x; y là số tự nhiên nên x + 5 ≥5 ; y + 2 ≥ 2. Khi đó (x+5)(y+2) = 51.2 = 34.3 = 6.17 = 17.6
Ta có bảng sau:
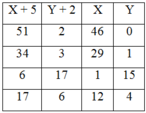
Vậy có các cặp nghiệm (x;y) thỏa mãn đề bài là: (46;0), (29;1), (1;15), (12;4)
28 tháng 10 2016
bài 3
( x + 5 ) . ( y + 2 ) = 102
ta có :\(y+2\inƯ\left(102\right)\)
mà \(y+2\ge2\)
nên \(y+2=2\)hoặc \(y+2=3\)
TH1 nếu \(y+2=2\)
=>\(y=1\)
Do \(y+2=2\)nên \(x+5=51\)
=>\(x=46\)
TH2 nếu \(y+2=3\)
=>\(y=1\)
Do \(y+2=3\)nên \(x+5=34\)
=>\(x=29\)
Vậy cặp số x;y lần lượt là :
nếu y=0 thì x=46
nếu y=1 thì x=29
B
26 tháng 8 2017
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
23 tháng 12 2021
\(xy+x+y=4\\ x\left(y+1\right)+y+1=4+1=5\\ \left(x+1\right)\left(y+1\right)=5\)
| \(x+1\) | \(5\) | \(1\) | \(-1\) | \(-5\) |
| \(y+1\) | \(1\) | \(5\) | \(-5\) | \(-1\) |
| \(x\) | \(4\) | \(0\) | \(-2\) | \(-6\) |
| \(y\) | \(0\) | \(4\) | \(-6\) | \(-2\) |
ta có x+5 là ước của 102 và lớn hơn hoặc bằng 5 nên
\(x+5\in\left\{17,34,51,102\right\}\)
từ đó ta tìm được các cặp (x,y) là \(\left(12,4\right);\left(29,1\right);\left(46,0\right)\)