A
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
1 tháng 12 2017
x n y n + 1 : x 2 y 5 = x n : x 2 y n + 1 : y 5 = x n - 2 . y n - 4 là phép chia hết
PT
1
PT
1
CM
19 tháng 3 2019
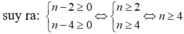
x 4 : x n = x 4 - n là phép chia hết nên 4 – n ≥ 0 ⇒ 0 ≤ n ≤ 4
suy ra: n ∈ {0; 1; 2; 3; 4}
PT
1
CM
10 tháng 4 2019
5 x n y 3 : 4 x 2 y 2 = 5/4 x n : x 2 y 3 : y 2 = 5/4 x n - 2 . y là phép chia hết
Suy ra: n – 2 ≥ 0 ⇒ n ≥ 2
CM
29 tháng 6 2017
Vì đa thức 5 x 3 - 7 x 2 + x chia hết cho 3 x n nên mỗi hạng tử của đa thức chia hết cho x n
=> hạng tử x – có số mũ nhỏ nhất của đa thức chia hết cho 3 x n
Do đó, x : x n ⇒ 0 ≤ x ≤ 1 . Vậy n ∈ {0; 1}
CM
26 tháng 11 2017
Vì đa thức 13 x 4 y 3 - 5 x 3 y 3 + 6 x 2 y 2 chia hết cho 5 x n y n nên mỗi hạng tử của đa thức trên chia hết cho 5 x n y n Do đó, hạng tử 6 x 2 y 2 chia hết cho 5 x n y n ⇒ 0 ≤ n ≤ 2 . Vậy n ∈ {0;1;2}
xnyn+1 : x2y5
=> n = 4
Làm đại ko chắc đúng
xnyn + 1 : x2y5
= (xn : x2)(yn + 1 : y5)
=> n - 4 \(\ge\)0
=> n \(\ge\) 4