Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có thể xây dựng cách phân tích thừa số đơn giản như sau: \(4018=2.2009\)
Từ đó, dễ dàng thành lập được một biểu thức số có dạng \(P=20092009...200940184018...4018\) luôn chia hết cho \(2009\) \(\text{(}\) với \(x\) là số các số \(2009,\) \(y\) là số các số \(4018\) \(\text{)}\)
Khi đó, tổng các chữ số cần tìm của \(P\) là \(\left(2+0+0+9\right).x+\left(4+0+1+8\right).y=11x+13y\)
Mặt khác, do \(P\) có tổng chữ số là \(2010\) hay nói cách khác \(11x+13y=2010\) \(\left(\alpha\right)\)
Ta phải cần tìm \(x,y\in Z^+\) để thỏa mãn điều kiện phương trình \(\left(\alpha\right)\) có nghiệm
Thật vậy, nhận thấy \(x=y=0\) không là nghiệm của phương trình \(\left(\alpha\right)\)
Do đó, từ \(\left(\alpha\right),\)suy ra \(x=\frac{2010-13y}{11}=183-y-\frac{2y+3}{11}\)
Để \(x\in N\) thì \(\frac{2y+3}{11}\in N\) tức là \(2y+3\inƯ\left(11\right)=\left\{-11;-1;1;11\right\}\)
Với chú ý rằng \(2y+3>3\) (do \(y>0\) ), kết hợp với điều ở trên, ta suy ra được \(2y+3=11\)
Hay \(y=8\) \(\left(\beta\right)\)
Từ \(\left(\alpha\right),\) \(\left(\beta\right)\) dễ dàng tính được \(x=178\) \(\left(\text{ t/m ĐK}\right)\)
Vậy, với \(P=20092009...200940184018...4018\) \(\text{(}\) trong đó, có \(178\) số \(2009,\) \(8\) số \(4018\) \(\text{)}\) thì thỏa mãn yêu cầu đề bài đã cho, nghĩa là có ít nhất một số tự nhiên tồn tại chia hết cho \(2009\) với tổng các chữ số là \(2010\)
CMR tồn tại 1 số tự nhiên chia hết cho 2009 có tổng các chữ số là 2010 2009

Vì n là số có 2 chữ số
→10≤n≤99→21≤2n+1≤199
Vì 2n+1 là số chính phương→2n+1∈{25;36;49,64;81;100;121;144;169;196}
Vì 2n+1 là số lẻ→2n+1∈{25;49;81;121;169}
Ta có bảng sau:
| 2n+1 | 25 | 49 | 81 | 121 | 169 |
| n | 12 | 24 | 40 | 60 | 84 |
| 3n+1 | 37 | 73 | 121 | 181 | 253 |
Với n=40 thì 2n+1=81 là số chính phương và 3n+1=121 là số chính phương
Vậy n=40
Vì n là số có 2 chữ số
\(\rightarrow10\le n\le99\)\(\rightarrow21\le2n+1\le199\)
Vì 2n+1 là số chính phương\(\rightarrow2n+1\in\left\{25;36;49,64;81;100;121;144;169;196\right\}\)
Vì 2n+1 là số lẻ\(\rightarrow2n+1\in\left\{25;49;81;121;169\right\}\)
Ta có bảng sau:
| 2n+1 | 25 | 49 | 81 | 121 | 169 |
| n | 12 | 24 | 40 | 60 | 84 |
| 3n+1 | 37 | 73 | 121 | 181 | 253 |
Với n=40 thì 2n+1=81 là số chính phương và 3n+1=121 là số chính phương
Vậy n=40

\(\frac{\left(-3\right)^n}{81}=-27\)
=> (-3)n = -27.81
=> (-3)n = -(27.81)
=> (-3)n = -(33.34)
=> (-3)n = -37 = (-3)7
=> n = 7
Vậy n = 7
\(\frac{\left(-3\right)^n}{81}=-27\)
\(\left(-3\right)^n:81=-27\)
\(\left(-3\right)^n=-27\cdot81\)
\(\left(-3\right)^n=-2187\)
\(\left(-3\right)^n=\left(-3\right)^7\)
\(=>n=7\)

Xet tam giac BDC va tam giac CEB ta co
^BDC = ^CEB = 900
BC _ chung
^BCD = ^CBE ( gt )
=> tam giac BDC = tam giac CEB ( ch - gn )
=> ^DBC = ^ECB ( 2 goc tuong ung )
Ta co ^B - ^DBC = ^ABD
^C - ^ECB = ^ACE
=> ^ABD = ^ACE
Xet tam giac IBE va tam giac ICD
^ABD = ^ACE ( cmt )
^BIE = ^CID ( doi dinh )
^BEI = ^IDC = 900
Vay tam giac IBE = tam giac ICD (g.g.g)
c, Do BD vuong AC => BD la duong cao
CE vuong BA => CE la duong cao
ma BD giao CE = I => I la truc tam
=> AI la duong cao thu 3
=> AI vuong BC

Giả sử tồn tại n sao cho n2 + 3n - 38 chia chết cho 49.
Khi đó: Xét biểu thức n2 - 4n + 4 = n2 + 3n - 7n - 38 + 42 = n2 + 3n - 38 - 7(n - 6) chia hết cho 7
Biểu thức đem xét là n2 - 4n + 4 viết -4n = -7n + 3n; 4 = -38 + 42
=> n2 - 4n + 4 = (n - 2)2 chia hết cho 7 hay n - 2 chia hết cho 7;
Gọi n - 2 = 7t => n = 2 + 7t. Thay vào S ta có:
S = (2 + 7t)2 + 3(2 + 7t) - 38 = 4 + 28t + 49t2 + 6 + 21t - 38 = 49t2 + 49t - 28
=> Không chia hết cho 49
=> ĐPCM
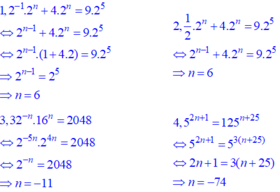

a)\(\frac{1}{2}.2^n+4.2^n=9.2^5\)
\(\Leftrightarrow2^n\left(\frac{1}{2}+4\right)=9.32\)
\(\Leftrightarrow2^n.\frac{9}{2}=288\)
\(\Leftrightarrow2^n=288:\frac{9}{2}\)
\(\Leftrightarrow2^n=64\)
\(\Leftrightarrow2^n=2^6\) \(\Rightarrow n=6\left(TMBT\right)\)
Vậy: n=6
b) \(3^2.3^{-5}.3^n=3^{11}\)
\(\Leftrightarrow3^{2+\left(-5\right)+n}=3^{11}\)
\(\Leftrightarrow3^{\left(-3\right)+n}=3^{11}\)
\(\Rightarrow\left(-3\right)+n=11\)
\(\Leftrightarrow n=11-\left(-3\right)\) \(\Rightarrow n=11+3\Rightarrow n=14\)
Vậy n=14
c) Câu c này bạn làm giống như câu a) nha bởi vì nó cũng giống nhau thôi, bạn biến đổi \(2^{-1}=\frac{1}{2}\)rồi làm giống như trên câu a) nhé.
P/s: mình mới học lớp 6 lên 7. sai chỗ nào thông cảm cho mik với nhé. luôn nhá..
Cảm ơn ạ!!