K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
25 tháng 12 2018
Số hạng thứ 5 trong khai triển
Nhận xét. Học sinh có thể nhầm số hạng thứ 5 ứng với k=5 nên là
Hoặc tính nhầm dẫn đến chọn A, hoặc chọn C
Chọn B
19 tháng 5 2017
Số hạng thứ \(k+1\) trong khai triển là :
\(t_{k+1}=C^k_{10}x^{10-k}\left(\dfrac{2}{x}\right)^k\)
Vậy \(t_5=C^4_{10}x^{10-4}.\left(\dfrac{2}{x}\right)^4=210.x^6.\dfrac{16}{x^4}=3360x^2\)
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 11 2021
\(C_n^0+C_n^1+C_n^2=11\)
\(\Rightarrow1+n+\dfrac{n\left(n-1\right)}{2}=11\)
\(\Leftrightarrow n^2+n-20=0\Rightarrow\left[{}\begin{matrix}n=4\\n=-5\left(loại\right)\end{matrix}\right.\)
\(\left(x^3+\dfrac{1}{x^2}\right)^4\) có SHTQ: \(C_4^k.x^{3k}.x^{-2\left(4-k\right)}=C_4^k.x^{5k-8}\)
\(5k-8=7\Rightarrow k=3\)
Hệ số: \(C_4^3=4\)
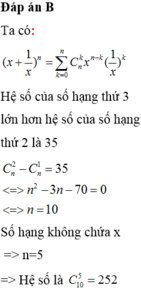
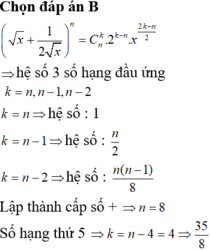
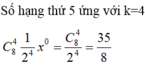
Số hạng thứ trong khai triển là
t 5 = 3360 x 2