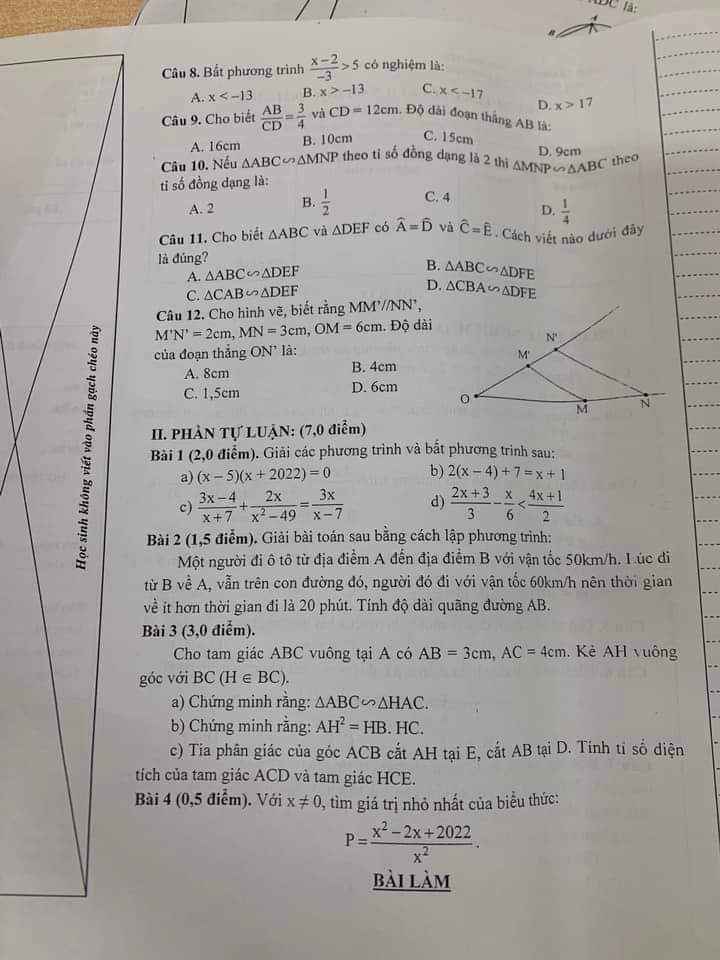Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 4:
\(P=\dfrac{x^2-2x+2022}{x^2}=\dfrac{2022x^2-2.2022x+2022^2}{2022x^2}=\dfrac{\left(x^2-2.2022x+2022^2\right)+2021x^2}{2022x^2}=\dfrac{\left(x-2022\right)^2}{2022x^2}+\dfrac{2021}{2022}\ge\dfrac{2021}{2022}\)\(P_{min}=\dfrac{2021}{2022}\Leftrightarrow x=2022\)

x3 - 2x2 + 6x = 12
x3 - 2x2 + 6x - 12 = 0
x2(x - 2) + 6(x - 2)=0
(x - 2)(x2 + 6) = 0
\(\Leftrightarrow \begin{bmatrix} x - 2 = 0 & & \\ x^{2} + 6 = 0& & \end{bmatrix}\) bỏ dấu ngoặc bên phải nha pn
\(\Leftrightarrow \begin{bmatrix} x = 2 & & \\ x^{2} = - 6 & & \end{bmatrix}\) không tìm được giá trị của x (pn ghi cái này kế pn chỗ x2 = - 6 nhé
Vậy x = 2
\(x^3-2x^2+6x=12\)
\(\Rightarrow\) \(x^3-2x^2+6x-12=0\)
\(\Rightarrow x^2\left(x-2\right)+6\left(x-2\right)=0\)
\(\Rightarrow\left(x-2\right)\left(x^2+6\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-2=0\\x^2+6=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=2\\x\in\varnothing\end{matrix}\right.\)
Vậy $x=2$

a+b+c=0<=>a^2+b^2+c^2+2ab+2bc+2ca=0
<=>a^2+b^2+b^c=-2ab-2bc-2ca
<=>(a^2+b^2+c^2)^2=4a^2b^2+4b^2c^2+4c^2a^2+8abc(a+b+c)
<=>(a^2+b^2+c^2)^2=4a^2b^2+4b^2c^2+4c^2a^2(vì a+b+c=0)(1)
(a^2+b^2+c^2)^2=4a^2b^2+4b^2c^2+4c^2a^2
<=>a^4+b^4+c^4+2a^2b^2+2b^2c^2+2c^2a^2=4a^2b^2+4b^2c^2+4c^2a^2
<=>a^4+b^4+c^4=2a^2b^2+2b^2c^2+2c^2a^2
<=>2(a^4+b^4+c^4)=4a^2b^2+4b^2c^2+4c^2a^2(2)
Từ (1) và (2)=>Đccm

Bài \(1.\)
\(x^4+2010x^2+2009x+2010=\left(x^4-x\right)+\left(2010x^2+2010x+2010\right)\)
\(=x\left(x^3-1\right)+2010\left(x^2+x+1\right)\)
\(=x\left(x-1\right)\left(x^2+x+1\right)+2010\left(x^2+x+1\right)\)
\(=\left(x^2+x+1\right)\left(x^2-x+2010\right)\)
Bài \(2.\)
\(x^2-25=y\left(y+6\right)\)
\(\Leftrightarrow\) \(x^2-25+9=y^2+6y+9\)
\(\Leftrightarrow\) \(x^2-16=\left(y+3\right)^2\)
\(\Leftrightarrow\) \(x^2-\left(y+3\right)^2=16\)
\(\Leftrightarrow\) \(\left(x-y-3\right)\left(x+y+3\right)=16\)
Bạn xét từng trường hợp nhóe!

Ta có:(n-3)(n+3)-(n-7)(n-3) (1)
=(n-3)(n+3-n+7)
=10(n-3)
Vậy PT(1) chia hết cho 10
\(\left(n-3\right)\left(n+3\right)-\left(n-7\right)\left(n-3\right)=\left(n-3\right)[n+3-\left(n-7\right)]\)
\(=\left(n-3\right)\left(n+3-n+7\right)=\left(n-3\right)\cdot10⋮10\)(ĐPCM)

\(x^2+3x+2\) =\(x^2+2.\frac{3}{2}x+\left(\frac{3}{2}\right)^2-\frac{5}{4}\)=\(\left(x+\frac{3}{2}\right)^2-\frac{5}{4}\ge-\frac{5}{4}\)
Dấu "=" xảy ra <=>\(x+\frac{3}{2}=0\)<=>\(x=-\frac{3}{2}\)
Bài 2:
a) \(x^2-4x+y^2+2y+5=0\)
=> \(\left(x^2-4x+4\right)+\left(y^2+2y+1\right)=0\)
=>\(\left(x-2\right)^2+\left(y+1\right)^2=0\)
Vì \(\left(x-2\right)^2+\left(y+1\right)^2\ge0\)nên:
=>\(\hept{\begin{cases}x-2=0\\y+1=0\end{cases}}\)<=>\(\hept{\begin{cases}x=2\\y=-1\end{cases}}\)
b)\(2x^2+y^2-2xy+10x+25=0\)
=>\(\left(x^2-2xy+y^2\right)+\left(x^2+10x+25\right)=0\)
=>\(\left(x-y\right)^2+\left(x+5\right)^2=0\)
Tới đây thì dễ nhá !

Có: \(8\left(a^2+b^2\right)=\left(2a+2b\right)^2\)
\(\Leftrightarrow8a^2+8b^2=4a^2+8ab+4b^2\)
\(\Leftrightarrow4a^2-8ab+4b^2=0\)
\(\Leftrightarrow a^2-2ab+b^2=0\)
\(\Leftrightarrow\left(a-b\right)^2=0\)
\(\Leftrightarrow a-b=0\Leftrightarrow a=b\)
=> đpcm
8(a2+b2) = (2a + 2b)2
=>8a2+8b2= 4a2 + 8ab + 4b
=> 4a2 + 4b2 = 8ab
=> 4a2 + 4b2 - 8ab = 0
=> (2a - 2b)2 =0
=> 2a - 2b = 0
=> 2(a-b)=0
=>a-b=0
=> a=b