HT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HT
2
7 tháng 5 2016
abcd = 1000 x a,bcd
abc,d = 100 x a,bcd
ab.cd = 10 x a,bcd
Nên:
abcd + abc,d + ab,cd + a,bcd = a,bcd x (1000 + 100 + 10 + 1) = 1111 x a,bcd
Hay
1111 x a,bcd = 2238,665
a,bcd = 2238,665 : 1111
a,bcd = 2,015
Vậy:
abcd = 2015
7 tháng 5 2016
Phải là abcd+abc,d+ab,cd+a,bcd=2238,665
abcd+abc,d+ab,cd+a,bcd=2238,665
=>1000 . a,bcd + 100 . a,bcd + 10 . a,bcd +a,bcd . 1 = 2238,665
=>a,bcd (1000+100+10+1) = 2238,665
=> 1111a,bcd = 2238,665
=> a,bcd = 2238,665 : 1111
=> a,bcd = 2,015
=> abcd = 2015
CM
25 tháng 2 2018
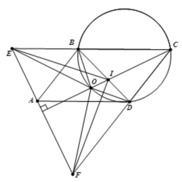
1). Tứ giác OBCD nội tiếp và CO là phân giác góc B C D ^ , suy ra O B D ^ = O C D ^ = O C B ^ = O D B ^ , nên tam giác OBD cân tại O, do đó OB=OD (1).
Tứ giác OBCD nội tiếp O D C ^ = O B E ^ (cùng bù với góc OBC) (2).
Trong tam giác CEF có CO vừa là đường cao vừa là đường phân giác nên tam giác CEF cân tại 
.
Do A B ∥ C F ⇒ A E B ^ = A F C ^ = E A B ^ , suy ra tam giác ABE cân tại B, nên B E = B A = C D ( 3 )
TA
15 tháng 4 2016
Gọi \(\overrightarrow{n}=\left(a,b\right)\) là vectơ pháp tuyến của CD (\(a^2+b^2\ne0\)
Ta có phương trình CD : \(ax+by+a+b=0\)
\(S_{BCD}=S_{ACD}=8\Rightarrow d\left(A;CD\right)=\frac{2.S}{CD}=2\Rightarrow d\left(M.CD\right)=1\)
\(\Rightarrow\frac{\left|2a-b\right|}{\sqrt{a^2+b^2}}=1\Leftrightarrow3a^2-4ab=0\)\(\rightarrow\begin{cases}a=0;b=1\\a=4;b=3\end{cases}\)\(\rightarrow\begin{cases}CD:y+1=0\\CD:4x+3y+7=0\end{cases}\)
Với \(CD:y+1=0\rightarrow D\left(d;-1\right);CD^2=4.AB^2=64\Leftrightarrow\begin{cases}d=7\\d=-9:L\end{cases}\)
\(D\left(7;-1\right);\overrightarrow{AB}=\frac{1}{2}\overrightarrow{DC}=\left(-4;0\right)\rightarrow B\left(-9;-3\right)\)
Với \(CD:4x+3y+7=0\rightarrow D\left(d;\frac{-4d-7}{3}\right)\rightarrow CD^2=\frac{25\left(d+1\right)^2}{9}=64\) (loại)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 12 2020
\(\overrightarrow{AC}.\overrightarrow{BD}=\left(\overrightarrow{AD}+\overrightarrow{DC}\right)\left(\overrightarrow{BA}+\overrightarrow{AD}\right)\)
\(=\overrightarrow{AD}.\overrightarrow{BA}+\overrightarrow{AD}^2+\overrightarrow{DC}.\overrightarrow{BA}+\overrightarrow{DC}.\overrightarrow{AD}\)
\(=\overrightarrow{AD}^2-\overrightarrow{AB}.\overrightarrow{DC}=a^2-a.2a=-a^2\)
Vì: abcd = 1000 x a,bcd
abc,d = 100 x a,bcd
ab.cd = 10 x a,bcd
Nên:abcd + abc,d + ab,cd + a,bcd = a,bcd x (1000 + 100 + 10 + 1) = 1111 x a,bcd
Hay :1111 x a,bcd = 2238,665
a,bcd = 2238,665 : 1111
a,bcd = 2,015
Vậy abcd=2015
abcd+abc,d+ab,cd+a,bcd=2238665
=>1000a+100b+10c+d+100a+10b+c+0,1d+10a+b+0,1c+0,01d+a+0,1b+0,01c+0,001d=2238665
=>1111a+111,1b+11,11c+1,111d=2238665
=>1111.(a+0,1b+0,01c+0,001d)=2238665
=>a,bcd=2015 (vô lý)
=> ko tìm dc abcd