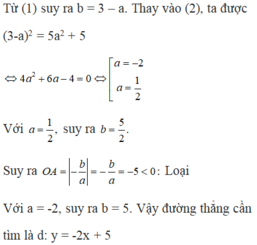Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do đường thẳng d đi qua điểm I (1; 3) nên a + b = 3 ⇒ a = 3 − b
Giao điểm của d và các tia Ox, Oy lần lượt là M ∈ − b a ; 0 và N 0 ; b
(Với b > 0, a < 0 suy ra b > 3)
Do đó: S Δ O M N = 1 2 . O M . O N = 1 2 . b a . b = b 2 2 a . Mà S Δ O M N = 6 ⇔ b 2 = 12 a
⇔ b 2 = 12 3 − b ⇔ b 2 = 36 − 12 b b 2 = − 36 + 12 b ⇔ b = 6 ( T M ) b = − 6 + 72 ( L ) b = − 6 − 72 ( L )
Với b = 6 ⇒ a = − 3 ⇒ d : y = − 3 x + 6
Đáp án cần chọn là: A

Đề thiếu dữ liệu quan trọng nhất là diện tích tam giác bằng bao nhiêu

Gọi ptđt (d) : y= ax +b (a≠ 0 )
Vì (d) tạo với hai tia Ox, Oy một tam giác vuông cân
nên A (0; b) và B (\(\dfrac{-b}{a}\); 0)
⇒ OA = b , OB = \(\dfrac{-b}{a}\)
ΔOAB vuông cân tại O
⇔ OA = OB
⇔ b = \(\dfrac{-b}{a}\)
⇔ a= -1
Mà I(2;3) ∈ (d) ⇔ 3= (-1) . 2 +b ⇔ b = 5
Vậy (d) : y = -x +5

Theo đề ta có : I\(\in\)d \(\Rightarrow\)2=a+b (1)
Lại có d tạo với hai tia Ox, Oy một tam giác diện tích bằng 4
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}x=0\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\text{y}\text{=}b\\x=\frac{-b}{a}\end{matrix}\right.\)
\(\Rightarrow\)S=\(\frac{1}{2}\frac{-b}{a}b=4\Leftrightarrow\frac{-b^2}{8}=a\:\left(2\right)\)
Thay (2) vào (1) ta co: \(b-\frac{b^2}{8}=2\:\Leftrightarrow8b-b^2-16=0\)
\(\Leftrightarrow b=4\:\Rightarrow\:a=-2\)
\(\Rightarrow\)d: y=-2x+4
Suy ra: A=(-2)2+42=20