
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(1,\\ b,\Leftrightarrow\left(x^2+4x+4\right)+\left(y-1\right)^2=25\\ \Leftrightarrow\left(x+2\right)^2+\left(y-1\right)^2=25\)
Vậy pt vô nghiệm do 25 ko phải tổng 2 số chính phương
\(2,\\ a,\Leftrightarrow x^2-\left(y^2-6y+9\right)=47\\ \Leftrightarrow x^2-\left(y-3\right)^2=47\)
Mà 47 ko phải hiệu 2 số chính phương nên pt vô nghiệm
\(b,\Leftrightarrow\left(x-2\right)^2+\left(3y-1\right)^2=16\)
Mà 16 ko phải tổng 2 số chính phương nên pt vô nghiệm
2b,
Vì 16 ko đồng dư với 1 (mod 4) nên 16 ko phải là tổng 2 scp
Định lý Fermat về tổng của hai số chính phương – Wikipedia tiếng Việt
vô đây đọc nhé


\(PT\Leftrightarrow\left(\frac{x-5}{2020}-1\right)+\left(\frac{x-6}{2019}-1\right)-\left(\frac{x-7}{2018}-1\right)-\left(\frac{x-8}{2017}-1\right)=0\)
\(\Leftrightarrow\left(x-2025\right)\left(\frac{1}{2020}+\frac{1}{2019}-\frac{1}{2018}-\frac{1}{2017}\right)=0\)
Dễ thấy \(\left(\frac{1}{2020}+\frac{1}{2019}-\frac{1}{2018}-\frac{1}{2017}\right)< 0\)
\(\Rightarrow x=2025=5^2.3^4\)
Vậy các ước nguyên tố của nghieemh pt là 3,5

Ta có: (x-2019)(x+2020)=0
\(\Leftrightarrow\left[{}\begin{matrix}x-2019=0\\x+2020=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2019\\x=-2020\end{matrix}\right.\)
Vậy: S={2019;-2020}

=>\(\left(\dfrac{x+1}{2021}+1\right)+\left(\dfrac{x+2}{2020}+1\right)+\left(\dfrac{x+3}{2019}+1\right)+\left(\dfrac{x+2028}{2}-3\right)=0\)
=>x+2022=0
=>x=-2022

\(\Rightarrow x+1+2x-2020=3x-2019\Leftrightarrow3x-2019=3x-2019\)
Vậy pt có vô số nghiệm

Nhận thấy vế trái luôn dương nên \(x-2020\ge0\Leftrightarrow x\ge2020\)
Với \(x\ge2020\Rightarrow\left\{{}\begin{matrix}x-2017\ge0\\2x-2018\ge0\\3x-2019\ge0\end{matrix}\right.\)
PT trở thành: \(x-2017+2x-2018+3x-2019=x-2020\)
Hay kết hợp với điều kiện \(x=\dfrac{4034}{5}\) suy ra PT đã cho vô nghiệm

Lời giải:
a.
PT $\Leftrightarrow (x+3)^2=2016^{2020}-17^{91}+9$
Ta thấy: $2016^{2020}-17^{91}+9\equiv 0-(-1)^{91}+0\equiv -1\equiv 2\pmod 3$
Mà 1 scp thì chia $3$ chỉ dư $0$ hoặc $1$ nên pt vô nghiệm.
b.
$x^2=2016(y-1)^2-2017^{2019}\equiv 0-1^{2019}\equiv 3\pmod 4$
Mà 1 scp chia $4$ chỉ dư $0$ hoặc $1$ nên vô lý.
Vậy pt vô nghiệm.
c.
$(x-1)^2=2017^{2017}+1\equiv 1^{2017}+1\equiv 2\pmod 4$
Mà 1 scp khi chia cho $4$ chỉ dư $0$ hoặc $1$ nên vô lý
Vậy pt vô nghiệm
d.
$(x+2)^2=2018^{10}+4\equiv (-1)^{10}+1\equiv 2\pmod 3$
Mà 1 scp khi chia $3$ dư $0$ hoặc $1$ nên vô lý
Vậy pt vô nghiệm.

Cho a,b,c khác 0 t/m:
1/a+1/b+1/c=1/2018 và a+b+c=2018
cmr" 1/a^2019+1/b^2019+1/c^2019=1/(a^2019+b^2019+c^2019)
Ta có :
Đến đây là dạng của phương trình ước số bạn chỉ cần xét ước của là sẽ tìm được nghiệm nguyên của

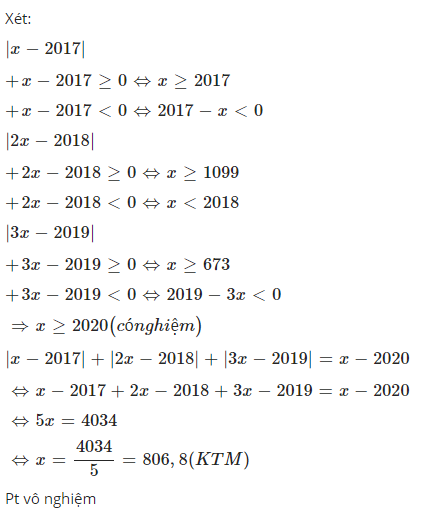
Nhận thấy \(x=\left\{2019;2020\right\}\) là 2 nghiệm của pt đã cho
- Với \(x>2020\Rightarrow\left\{{}\begin{matrix}\left|x-2019\right|^{2019}>1\\\left|x-2020\right|^{2020}>0\end{matrix}\right.\) \(\Rightarrow VT>1>VP\)
\(\Rightarrow\) pt vô nghiệm
- Với \(x< 2019\Rightarrow\left\{{}\begin{matrix}\left|x-2019\right|^{2019}>0\\\left|x-2020\right|^{2020}>1\end{matrix}\right.\) \(\Rightarrow VT>1>VP\)
Pt vô nghiệm
- Với \(2019< x< 2020\Rightarrow\left\{{}\begin{matrix}0< x-2019< 1\\0< 2020-x< 1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left|x-2019\right|^{2019}< x-2019\\\left|2020-x\right|^{2020}< 2020-x\end{matrix}\right.\)
\(\Rightarrow VT< x-2019+2020-x=1\Rightarrow VT< VP\)
Pt vô nghiệm
Vậy pt có đúng 2 nghiệm \(\left[{}\begin{matrix}x=2019\\x=2020\end{matrix}\right.\)
giỏi quá