K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
13 tháng 4 2022
Bài 1.
a.\(\left(x-8\right)\left(x^3+8\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-8=0\\x^3+8=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-2\end{matrix}\right.\)
b.\(\left(4x-3\right)-\left(x+5\right)=3\left(10-x\right)\)
\(\Leftrightarrow4x-3-x-5=30-3x\)
\(\Leftrightarrow4x-x+3x=30+5+3\)
\(\Leftrightarrow6x=38\)
\(\Leftrightarrow x=\dfrac{19}{3}\)
AH
Akai Haruma
Giáo viên
13 tháng 4 2022
Bài 1:
a. $(x-8)(x^3+8)=0$
$\Rightarrow x-8=0$ hoặc $x^3+8=0$
$\Rightarrow x=8$ hoặc $x^3=-8=(-2)^3$
$\Rightarrow x=8$ hoặc $x=-2$
b.
$(4x-3)-(x+5)=3(10-x)$
$4x-3-x-5=30-3x$
$3x-8=30-3x$
$6x=38$
$x=\frac{19}{3}$
11 tháng 7 2015
a) Thay đa thức này bằng 0, ta được:
f(x) = x^3 - x^2 + x - 1 = 0
=> f(x) = x . x2 - x . x + x - 1 = 0
=> f(x) = x. (x2 - x + x) = 0 + 1 = 1
=> f(x) = x . x2 = 1
=> x = 1 và x2 = 1
=> x = 1
Vậy nghiệm của đa thức là x = 1
NT
0
12 tháng 7 2015
a)g(x)=0=>11x3+5x2+4x+10=0
=>(10x3+10)+(x3+x2)+(4x2+4x)=0
=>10(x3+1)+x2(x+1)+4x(x+1)=0
=>10(x+1)(x2−x+1)+x2(x+1)+4x(x+1)=0
=>(x+1)[(10(x2−x+1)+x2+4x]=0
=>(x+1)(11x2−6x+10)=0
=>(x+1)[(9x2−2.3x+1)+2x2+9]=0
=>(x+1)[(3x−1)2+2x2+9]=0
=>x+1=0
=>x=-1
Vậy x=-1
NT
2
1 tháng 5 2015
f(x) = 0 => x3 - 2x2 - x + 2 = 0
=> x2. (x - 2) - (x - 2) = 0
=> (x2 - 1).(x - 2) = 0 => x2 - 1 = 0 hoặc x - 2 = 0
+) x2 - 1 = 0 => x = 1 hoặc x = -1
+) x - 2 = 0 => x = 2
Vậy đa thức có 3 nghiệm là: -1;1;2
22 tháng 4 2018
\(a)\) Ta có :
\(A=\frac{1}{x^2-4x+7}\)
\(A=\frac{1}{\left(x^2-4x+4\right)+3}\)
\(A=\frac{1}{\left(x-2\right)^2+3}\)
Lại có :
\(\left(x-2\right)^2\ge0\)
\(\Rightarrow\)\(\left(x-2\right)^2+3\ge3\)
\(\Rightarrow\)\(A=\frac{1}{\left(x-2\right)^2+3}\le\frac{1}{3}\)
Dấu "=" xảy ra khi và chỉ khi \(\left(x-2\right)^2+3=3\)
\(\Leftrightarrow\)\(\left(x-2\right)^2=3-3\)
\(\Leftrightarrow\)\(\left(x-2\right)^2=0\)
\(\Leftrightarrow\)\(x-2=0\)
\(\Leftrightarrow\)\(x=2\)
Vậy GTLN của \(A\) là \(\frac{1}{3}\) khi 2\(x=2\)
Chúc bạn học tốt ~
22 tháng 4 2018
\(b)\) Ta có :
\(f\left(x\right)=x^2-4x+7\)
\(f\left(x\right)=\left(x^2-4x+4\right)+3\)
\(f\left(x\right)=\left(x-2\right)^2+3\ge3>0\)
Vậy đa thức \(f\left(x\right)\) vô nghiệm
Chúc bạn học tốt ~
AH
Akai Haruma
Giáo viên
22 tháng 4 2021
Lời giải:
$M(x)=(6+4x)(-x+2)=0$
\(\Leftrightarrow \left[\begin{matrix} 6+4x=0\\ -x+2=0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=-\frac{3}{2}\\ x=2\end{matrix}\right.\)
Vậy nghiệm của đa thức $M(x)$ là $x=\frac{-3}{2}$ và $x=2$
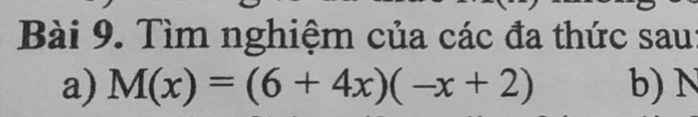
Ta có :
\(f\left(x\right)-g\left(x\right)=4x+\frac{16}{3}\)
\(\Rightarrow4x+\frac{16}{3}=0\)
\(\Rightarrow4x=0-\frac{16}{3}\)
\(\Rightarrow4x=\frac{-16}{3}\)
\(\Rightarrow x=\frac{-16}{3}\div4\)
\(\Rightarrow x=\frac{-4}{3}\)
Vậy nghiệm của đa thức f (x) - g(x) là \(\frac{-4}{3}\)