
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ta có: \(5x^2+\left(x^2-2.\frac{3}{2}x+\frac{9}{4}\right)-\frac{45}{4}\)
=>\(5x^2\ge0\forall x,\left(x-\frac{3}{2}\right)^2\ge0\)
=>\(6x^2-3x-9\ge9\)
=>vô nghiệm

Nêu da thúc do co nghiệm Nguyen thi se la ước cua he so tu do hay la 10 ma ước 10 la +-1,+-2,+-5,+-10
neu x=1=> da thúc co gia tri la 5 khác 0
neu x=-1 => da thúc bang 17 khác 0
neu x=2 => d thúc bang 14 khác 0
neu x=-2 => da thúc bang 38 khác 0
neu x=5=> da thúc bang 605 khác 0
neu x=-5=> da thúc bang 665 khác 0
neu x=10=> da thúc bang 9950 khác 0
neu x=-10 => da thúc bang 10070 khác 0
vay da thúc do ko co nghiem

Để có nghiệm của đa thức thì \(-6x+14=0\)
\(-6x=0-14\)
\(-6x=-14\)
\(x=\frac{-14}{-6}\)
\(x=\frac{7}{3}\)
Ta có : -6x + 14 = 0
-6x = -14
x = -14 : (-6)
x = \(\frac{7}{3}\)
Vậy x = \(\frac{7}{3}\)là nghiệm của đa thức.
Chúc bạn học tốt


Lời giải:
$M(x)=(6+4x)(-x+2)=0$
\(\Leftrightarrow \left[\begin{matrix} 6+4x=0\\ -x+2=0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=-\frac{3}{2}\\ x=2\end{matrix}\right.\)
Vậy nghiệm của đa thức $M(x)$ là $x=\frac{-3}{2}$ và $x=2$

\(a,P\left(x\right)=2x^3-3x+7-x=2x^3-4x+7\\ Q\left(x\right)=-5x^3+2x-3+2x-x^2-2=-5x^3-x^2+4x-5\)
\(M\left(x\right)=2x^3-4x+7+\left(-5x\right)^3-x^2+4x-5=-3x^3-x^2+2\)
\(N\left(x\right)=2x^3-4x+7-\left(-5x\right)^3+x^2-4x+5=7x^3+x^2-8x+12\)
b,\(M\left(x\right)=-3x^3-x^2+2=0\)
Nghiệm xấu lắm bạn

\(2x^2-4x+5=2\left(x^2-2x+\frac{5}{2}\right)=2\left[\left(x^2-2x+1\right)+\frac{3}{2}\right]=2\left[\left(x-1\right)^2+\frac{3}{2}\right]=2\left(x-1\right)^2+3\ge3\)
\(\Rightarrow x\in\phi\)

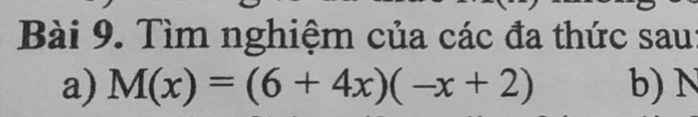
Nghiệm của đa thức làm cho:\(x^2-6x+5=0\Leftrightarrow x^2-x-5x+5=0\)
\(\Rightarrow x\left(x-1\right)-5\left(x-1\right)=0\Leftrightarrow\left(x-1\right)\left(x-5\right)=0\)\(\Rightarrow\orbr{\begin{cases}x-1=0\\x-5=0\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=1\\x=5\end{cases}}\)
Tập nghiệm của pt S={1,5}
Ta có :
\(x^2-6x+5=0\)
\(\Leftrightarrow\left(x^2-6x+9\right)-4=0\)
\(\Leftrightarrow\left(x-3\right)^2-2^2=0\)
\(\Leftrightarrow\left(x-3-2\right)\left(x-3+2\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-1=0\\x-5=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=1\\x=5\end{cases}}\)
Vậy \(x\in\left\{1;5\right\}\)