K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
1
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 4 2021
Xét pt (1): \(6x-5m=3+3mx\Leftrightarrow\left(3m-6\right)x=-5m-3\)
Để pt có nghiệm \(\Rightarrow m\ne2\) khi đó \(x=\dfrac{-5m-3}{3m-6}\)
Xét pt (2): \(\left(x+1\right)\left(x-1\right)-\left(x+2\right)^2=3\)
\(\Leftrightarrow x^2-1-x^2-4x-4=3\Rightarrow4x=-8\Rightarrow x=-2\)
Để nghiệm của (1) gấp 2 lần nghiệm của (2)
\(\Rightarrow\dfrac{-5m-3}{3m-6}=-2.2=-4\)
\(\Leftrightarrow-5m-3=-12m+24\Rightarrow m=\dfrac{27}{7}\)
29 tháng 4 2017
bạn ko nên đăng các câu ko liên quan đến toán học như vậy!
10 tháng 11 2021
\(1,Sửa:A=4x^4+4x^2y+y^2+2=\left(2x^2+y\right)^2+2\ge2\\ A_{min}=2\Leftrightarrow2x^2+y=0\Leftrightarrow x^2=-\dfrac{y}{2}\\ 2,B=\left(x+y\right)^2+\left(y+1\right)^2+12\ge12\\ B_{min}=12\Leftrightarrow\left\{{}\begin{matrix}x=-y=1\\y=-1\end{matrix}\right.\)
NB
2
TT
6 tháng 3 2020
Ta có : \(x^2+y^2\ge2xy\)
\(\Leftrightarrow2\left(x^2+y^2\right)\ge\left(x+y\right)^2\)
\(\Leftrightarrow x^2+y^2\ge\frac{\left(x+y\right)^2}{2}\)
Áp dụng vào bài toán có :
\(P\le\frac{x+y}{\frac{\left(x+y\right)^2}{2}}+\frac{y+z}{\frac{\left(y+z\right)^2}{2}}+\frac{z+x}{\frac{\left(z+x\right)^2}{2}}\) \(=\frac{2}{x+y}+\frac{2}{y+z}+\frac{2}{z+x}=\frac{1}{2}\left(\frac{4}{x+y}+\frac{4}{y+z}+\frac{4}{z+x}\right)\)
Áp dụng BĐT Svacxo ta có :
\(\frac{4}{x+y}\le\frac{1}{x}+\frac{1}{y}\), \(\frac{4}{y+z}\le\frac{1}{y}+\frac{1}{z}\), \(\frac{4}{z+x}\le\frac{1}{z}+\frac{1}{x}\)
Do đó : \(P\le\frac{1}{2}\left[2.\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)\right]=2016\)
Dấu "=" xảy ra \(\Leftrightarrow x=y=z=\frac{1}{672}\)
P/s : Dấu "=" không chắc lắm :))
KR
7 tháng 5 2018
Áp dụng Bunyakovsky, ta có :
\(\left(1+1\right)\left(x^2+y^2\right)\ge\left(x.1+y.1\right)^2=1\)
=> \(\left(x^2+y^2\right)\ge\frac{1}{2}\)
=> \(Min_C=\frac{1}{2}\Leftrightarrow x=y=\frac{1}{2}\)
Mấy cái kia tương tự
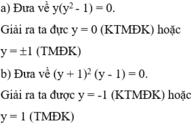
x=+-1
y=0
\(x^2-y^2=y+1\)
\(\Leftrightarrow4x^2-4y^2-4y-4=0\)
\(\Leftrightarrow4x^2-\left(2y+1\right)^2=3\)
\(\Leftrightarrow\left(2x-2y-1\right)\left(2x+2y+1\right)=3\)
\(\Leftrightarrow\hept{\begin{cases}2x+2y+1=1\\2x-2y-1=3\end{cases}}\)hoặc \(\hept{\begin{cases}2x+2y+1=3\\2x-2y-1=1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=1\\y=-1\end{cases}\left(l\right)}\)hoặc \(\hept{\begin{cases}x=1\\y=0\end{cases}\left(nhan\right)}\)