Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có 2 2 n + 1 = 1 + 1 2 n + 1 = C 2 n + 1 0 + C 2 n + 1 1 + ... + C 2 n + 1 2 n + 1 . (1)
Lại có C 2 n + 1 0 = C 2 n + 1 2 n + 1 ; C 2 n + 1 1 = C 2 n + 1 2 n ; C 2 n + 1 2 = C 2 n + 1 2 n − 1 ; . . . ; C 2 n + 1 n = C 2 n + 1 n + 1 . (2)
Từ (1) và (2), suy ra C 2 n + 1 0 + C 2 n + 1 1 + ... + C 2 n + 1 n = 2 2 n + 1 2
⇔ C 2 n + 1 1 + ... + C 2 n + 1 n = 2 2 n + 1 2 − C 2 n + 1 0
⇔ C 2 n + 1 1 + ... + C 2 n + 1 n = 2 2 n − 1 ⇔ 2 20 − 1 = 2 2 n − 1 ⇔ n = 10 .
Vậy n =10 thỏa mãn yêu cầu bài toán.
Chọn đáp án C.

Xét khai triển x + 1 2 n + 1 = C 2 n + 1 0 x 2 n + 1 + C 2 n + 1 1 x 2 n + ... + C 2 n + 1 2 n + 1 .
Cho x =1 , ta được 2 2 n + 1 = C 2 n + 1 0 + C 2 n + 1 1 + ... + C 2 n + 1 2 n + 1 .(1)
Cho x= -1, ta được 0 = − C 2 n + 1 0 + C 2 n + 1 1 − ... + C 2 n + 1 2 n + 1 . (2)
Cộng (1) và (2) vế theo vế, ta được :
2 2 n + 1 = 2 C 2 n + 1 1 + C 2 n + 1 3 + ... + C 2 n + 1 2 n + 1 ⇔ 2 2 n + 1 = 2.1024 = 2 11 ⇔ 2 n + 1 = 11 ⇔ n = 5 .
Chọn đáp án A.

Ta có:
\(n^5+n^4-2n^3-2n^2+1=p^k\Leftrightarrow\left(n^2+n-1\right)\left(n^3-n-1\right)=p^k\)
Từ gt \(\Rightarrow n,k\ge2\)
Ta có:
\(\left\{{}\begin{matrix}n^3-n-1>1;n^2+n-1>1,\forall n\ge2\\\left(n^3-n-1\right)-\left(n^2+n-1\right)=\left(n+1\right)n\left(n-2\right)\ge0,\forall n\ge2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}n^3-n-1=p^r\\n^2+n-1=p^s\end{matrix}\right.\) trong đó \(\left\{{}\begin{matrix}r\ge s>0\\r+s=k\end{matrix}\right.\)
\(\Rightarrow n^3-n-1⋮n^2+n-1\)
\(\Rightarrow n^3-n-1-\left(n-1\right)\left(n^2+n-1\right)⋮n^2+n-1\)
\(\Rightarrow n-2⋮n^2+n-1\) (1)
Mặt khác:
\(\left(n^2+n-1\right)-\left(n-2\right)=n^2+1>0,\forall n\)
\(\Rightarrow n^2+n-1>n-2\ge0,\forall n\ge2\) (2)
Từ (1) và (2) => n=2 => \(p^k=25\Rightarrow\left\{{}\begin{matrix}p=5\\k=2\end{matrix}\right.\)
Vậy bộ số (n,k,p)=(2,2,5)
\(...\Leftrightarrow\left(n^2+n-1\right)\left(n^3-n-1\right)=p^k\).
Do đó \(\left\{{}\begin{matrix}n^2+n-1=p^v\\n^3-n-1=p^u\end{matrix}\right.\left(v,u\in N;v+u=k\right)\).
+) Với n = 2 ta có \(p^k=25=5^2\Leftrightarrow p=5;k=2\)
+) Với n > 2 ta có \(n^3-n-1>n^2+n-1\Rightarrow v>u\Rightarrow n^3-n-1⋮n^2+n-1\)
\(\Rightarrow\left(n^2+n-1\right)\left(n-1\right)+n-2⋮n^2+n-1\)
\(\Rightarrow n-2⋮n^2+n-1\)
\(\Rightarrow\left(n-2\right)\left(n+3\right)⋮n^2+n-1\)
\(\Rightarrow6⋮n^2+n-1\).
Không tồn tại n > 2 thoả mãn
Vậy...

Ta có:
\(n^5+n^4-2n^3-2n^2+1=p^k\Leftrightarrow\left(n^2+n-1\right)\left(n^3-n-1\right)=p^k\)
Từ giả thiết \(\Rightarrow n,k\ge2\)
Ta có:
\(\hept{\begin{cases}n^3-n-1>1,n^2+n-1>1,\forall n\ge2\\\left(n^3-n-1\right)-\left(n^2+n-1\right)=\left(n+1\right)n\left(n-2\right)\ge0,\forall n\ge2\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}n^3-n-1=p^r\\n^2+n-1=p^s\end{cases}}\) trong đó \(\hept{\begin{cases}r\ge s\ge0\\r+s=k\end{cases}}\)
\(\Rightarrow n^3-n-1⋮n^2+n-1\)
\(\Rightarrow n^3-n-1-\left(n-1\right)\left(n^2+n-1\right)⋮n^2+n-1\)
\(\Rightarrow n-2⋮n^2+n-1\) (1)
Mặt khác :
\(\left(n^2+n-1\right)-\left(n-2\right)=n^2+1>0,\forall n\)
\(\Rightarrow n^2+n-1>n-2\ge0,\forall n\ge2\) (2)
Từ (1) và (2) => n=2 => \(p^k=25\Rightarrow\hept{\begin{cases}p=5\\k=2\end{cases}}\)
Vậy bộ số cần tìm là (n,k,p)=(2,2,5)


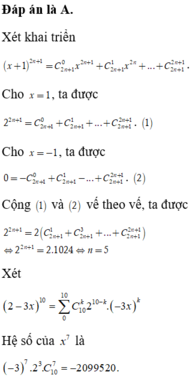


A mình biết làm rồi nên thôi ạ. Cảm ơn mọi người!!! Cứ đăng câu hỏi xong lại biết làm hic