Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/
\(y'=-\frac{4}{\left(x-2\right)^2}\Rightarrow\left\{{}\begin{matrix}y'\left(3\right)=-4\\y\left(3\right)=6\end{matrix}\right.\)
Pt tiếp tuyến: \(y=-4\left(x-3\right)+6\Leftrightarrow y=-4x+18\)
b.
\(y'=\frac{-5}{\left(x-1\right)^2}\)
Tiếp tuyến song song với \(y=-5x-3\) nên có hệ số góc \(k=-5\)
\(\Rightarrow\frac{-5}{\left(x-1\right)^2}=-5\Rightarrow\left(x-1\right)^2=1\Rightarrow\left[{}\begin{matrix}x=2\\x=0\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn

+Ta có đạo hàm y’ = 3x2- 6mx+ 3( m+ 1) .
Do K thuộc ( C) và có hoành độ bằng -1, suy ra K( -1; -6m-3)
Khi đó tiếp tuyến tại K có phương trình
∆: y= ( 9m+ 6) x+ 3m+ 3
Đường thẳng ∆ song song với đường thẳng d
⇒ 3 x + y = 0 ⇔ y = - 3 x ⇔ 9 m + 6 = - 3 3 m + 3 ≠ 0 ⇔ m = - 1 m ≠ - 1
Vậy không tồn tại m thỏa mãn đầu bài.
Chọn D.

Tiếp tuyến d của đồ thị hàm số tại điểm có hoành độ x = -1, có dạng :
\(y=\left(m+1\right)x+\frac{m}{2}+1\)
D song song với đường thẳng y = 5x\(\Leftrightarrow\begin{cases}m+1=5\\\frac{m}{2}+1\ne0\end{cases}\)\(\Leftrightarrow m=4\)
Vậy m = 4 là giá trị cần tìm

Ta có \(M\left(-1;-2\right)\)
Phương trình của (C) tại M là \(\Delta:y=y'\left(-1\right)\left(x+1\right)-2\)
hay \(\Delta:y=9x+7\)
\(\Delta\) // d \(\Leftrightarrow\begin{cases}m^2+5=9\\3m+1\ne7\end{cases}\) \(\Leftrightarrow\begin{cases}m=\pm2\\m\ne2\end{cases}\) \(\Leftrightarrow m=-2\)

a. Tiếp tuyến của \(\left(C_m\right)\) tại điểm có hoành độ x = 1 có phương trình :
\(y=\left(m-2\right)\left(x-1\right)+3m-2=\left(m-2\right)x+3m\)
Yêu cầu của bài toán khi và chỉ khi \(\begin{cases}m-2=3\\2m\ne10\end{cases}\) vô nghiệm
Vậy không tồn tại m thỏa mãn yêu cầu bài toán
b. Ta có \(y'=3\left(x^2-\frac{4}{3}x+\frac{4}{9}\right)+m-\frac{7}{3}=3\left(x-\frac{2}{3}\right)^2+m-\frac{7}{3}\)
Suy ra \(y'\ge m-\frac{7}{3}\)
Tiếp tuyến tại điểm có hoành độ \(x=\frac{2}{3}\) có hệ số góc nhỏ nhất và hệ số góc có giá trị \(k=m-\frac{7}{3}\)
Yêu cầu bài toán \(\Leftrightarrow k.2=-1\Leftrightarrow\left(m-\frac{7}{3}\right).2=-1\Leftrightarrow m=\frac{11}{6}\)

Tập xác định \(D=R\backslash\left\{2-m\right\}\)
Ta có : \(y'=\frac{m^2-2m-1}{\left(x+m-2\right)^2}\)
a) Tiếp tuyến tại điểm có hoành độ x = 1 song song với đường thẳng :
\(y=x+1\) khi \(y'\left(1\right)=-1\Leftrightarrow\frac{m^2-2m-1}{\left(x+m-2\right)^2}=-1\Leftrightarrow m=0;m=2\)
* Với m = 0 ta có phương trình tiếp tuyến \(y=-\left(x-1\right)-1=-x\)
* Với m = 2 ta có phương trình tiếp tuyến \(y=-\left(x-2\right)+3=-x+5\)
Vậy m = 0 là giá trị cần tìm
b) G\(m\ge1+\sqrt{2};m\le1-\sqrt{2}\)ọi \(M\left(x_0;y_0\right)\) là tiếp điểm. Ta có \(y'\left(x_0\right)=-\frac{1}{2}\)
\(\frac{m^2-2m-1}{\left(x_0+m-2\right)^2}=-\frac{1}{2}\) (*)
Yêu cầu bài toán suy ra (*) vô nghiệm, điều đó xảy ra khi :
\(m^2-2m-1\ge0\Leftrightarrow\left[\begin{array}{nghiempt}m\ge1+\sqrt{2}\\m\le1-\sqrt{2}\end{array}\right.\)
Vậy giá trị cần tìm là \(m\le1-\sqrt{2};m\ge1+\sqrt{2}\)

1.
Tiếp tuyến vuông góc với \(y=-x+2017\) nên có hệ số góc \(k=\frac{-1}{-1}=1\)
\(y'=3x^2-4x+2=1\)
\(\Rightarrow3x^2-4x+1=0\Rightarrow\left[{}\begin{matrix}x=1\\x=\frac{1}{3}\end{matrix}\right.\)
\(\Rightarrow x_1+x_2=1+\frac{1}{3}=\frac{4}{3}\)
2.
Tiếp tuyến song song Ox nên có hệ số góc \(k=0\)
\(y'=3x^2-3=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
3.
\(y'=x^2+6x=-9\Rightarrow\left(x+3\right)^2=0\Rightarrow x=-3\Rightarrow y=16\)
Pt tiếp tuyến: \(y=-9\left(x+3\right)+16=-9x-11\)
4.
Tiếp tuyến vuông góc \(y=\frac{1}{9}x+2017\) có hệ số góc \(k=\frac{-1}{\frac{1}{9}}=-9\)
\(y'=-3x^2+6x=-9\Leftrightarrow3x^2-6x-9=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)
Có 2 tiếp điểm nên có 2 tiếp tuyến thỏa mãn

Câu 1:
\(f'\left(1\right)=g'\left(1\right)=k\)
\(h\left(x\right)=\frac{f\left(x\right)+2}{g\left(x\right)+1}\Rightarrow h'\left(x\right)=\frac{f'\left(x\right)\left[g\left(x\right)+1\right]-g'\left(x\right)\left[f\left(x\right)+2\right]}{\left[g\left(x\right)+1\right]^2}\)
\(\Rightarrow h'\left(1\right)=\frac{k\left(b+1\right)-k\left(a+2\right)}{\left(b+1\right)^2}=\frac{k\left(b-a-1\right)}{\left(b+1\right)^2}\)
Mà \(h'\left(1\right)=k\Rightarrow k=\frac{k\left(b-a-1\right)}{\left(b+1\right)^2}\Rightarrow\frac{b-a-1}{\left(b+1\right)^2}=1\)
\(\Leftrightarrow b-a-1=\left(b+1\right)^2\Rightarrow a=b-1-\left(b+1\right)^2\)
\(\Rightarrow a=-b^2-b-2\)
Câu 2:
\(y=f\left(x\right)=\frac{x+1}{x-2}\Rightarrow f'\left(x\right)=\frac{-3}{\left(x-2\right)^2}\)
Phương trình hoành độ giao điểm:
\(\frac{x+1}{x-2}=x+m\Leftrightarrow x+1=\left(x+m\right)\left(x-2\right)\)
\(\Leftrightarrow x^2+\left(m-3\right)x-2m-1=0\)
\(\Delta=\left(m-3\right)^2+4\left(2m+1\right)=\left(m+1\right)^2+12>0\)
\(\Rightarrow\) d luôn cắt (P) tại 2 điểm phân biệt A và B có hoành độ giả sử là a và b
Theo Viet: \(\left\{{}\begin{matrix}a+b=3-m\\ab=-3m-1\end{matrix}\right.\) \(\Rightarrow3a+3b-ab=10\) (1)
Mặt khác do tiếp tuyến tại A và B song song
\(\Leftrightarrow\frac{-3}{\left(a-2\right)^2}=\frac{-3}{\left(b-2\right)^2}\Leftrightarrow\left[{}\begin{matrix}a-2=b-2\\a-2=2-b\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}a=b\\a=4-b\end{matrix}\right.\)
TH1: \(a=b\) thay vào (1):
\(\Rightarrow-a^2+6a-10=0\left(vn\right)\)
TH2: \(a=4-b\)
\(\Rightarrow a+b=4\Rightarrow3-m=4\Rightarrow m=-1\)
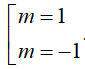
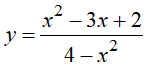 là:
là: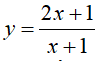 có đồ thị (C). Tìm các điểm M trên đồ thị (C) sao cho khoảng cách từ hai điểm A(2;4) và B(-4;-2) đến tiếp tuyến của (C) tại M là bằng nhau
có đồ thị (C). Tìm các điểm M trên đồ thị (C) sao cho khoảng cách từ hai điểm A(2;4) và B(-4;-2) đến tiếp tuyến của (C) tại M là bằng nhau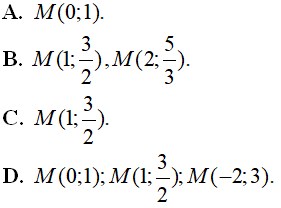 giúp mik nhe r mik tick choa pls
giúp mik nhe r mik tick choa pls