TT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
30 tháng 6 2017
Đáp án A
Phương pháp: Chia cả 2 vế cho 3x, đặt 
, tìm điều kiện của t.
Đưa về bất phương trình dạng 
Cách giải :
Ta có 
Đặt 
, khi đó phương trình trở thành
Ta có: 
Vậy 
24 tháng 2 2016
*x2+bx+c=0
\(\Delta=b^2-4c=b^2-4.\left(2b-4\right)=b^2-8b+16=\left(b-4\right)^2\)=>\(\sqrt{\Delta}=\left|b-4\right|\)
Với (b-4)2=0 =>b=4 =>c=4
PT có 1 nghiệm kép: \(x_1=x_2=-2\)
Với\(\Delta=\) (b-4)2>0,PT có 2 nghiệm pb: \(x_1=\frac{-b+\left|b-4\right|}{2};x_2=\frac{-b-\left|b-4\right|}{2}\)
Với b>4 thì: \(x_1=-2;x_2=\frac{-2b+4}{2}=-b+2\)
Với b<0 thì: x1=-b+2 ; x2=-2
Vậy khi c=2b-4 và b tùy ý thì PT: x2+bx+c=0 luôn có 1 nghiệm nguyên là -2
CM
3 tháng 3 2017
Đáp án C
4 − x + 4 + x 3 − 6 16 − x 2 + 2 m + 1 = 0 (*) ĐK x ∈ − 4 ; 4
Đặt S = 4 − x + 4 + x , S ∈ 2 2 ; 4 P = 4 − x . 4 + x = 16 − x 2 , P ∈ 0 ; 4
Khi đó phương trình đã cho trở thành
S 3 − 6 P + 2 m + 1 = 0 S 2 = 2 P + 8 ⇔ P = S 2 − 8 2 S 3 − 6 S 2 − 8 2 + 2 m + 1 = 0 ⇔ P = S 2 − 8 2 ( 1 ) S 3 − 3 S 2 + 24 + 2 m + 1 = 0 ( 2 )
Để phương trình (*) có nghiệm
hệ phương trình trên có nghiệm S ≥ 2 2 , P ≥ 0 và S 2 > 4 P
phương trình (2) có nghiệm S ∈ 2 2 ; 4
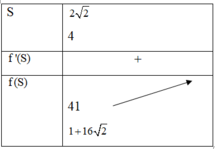
f ( S ) = S 3 − 3 S 2 + 25, S ∈ 2 2 ; 4 f ' ( S ) = 3 S 2 − 6 S f ' ( S ) = 0 ⇔ S = 0 ( L ) S = 2 ( L )
Bảng biến thiên
27 tháng 2 2016
hệ :\(\Leftrightarrow\begin{cases}\left(m-3\right)x\le m+1\\\left(2m+1\right)\le2m\end{cases}\)
suy ra hệ này có nghiệm duy nhất:
\(\Leftrightarrow\frac{m+1}{m-3}=\frac{2m}{2m+1}\Leftrightarrow\)\(\left(m+1\right)\left(2m+1\right)=2m\left(m-3\right)\)
\(\Leftrightarrow2m^2+m+2m+1=2m^2-6m\)
\(\Leftrightarrow m=-\frac{1}{9}\in\left(-\frac{1}{2};3\right)\)
nếu \(m=3\) thì hệ \(\Leftrightarrow\begin{cases}0\le4\\7x\le6\end{cases}\)có vô số nghiệm
nếu \(m=-\frac{1}{2}\) thì hệ \(\Leftrightarrow\begin{cases}-\frac{7}{2}x\le\frac{1}{2}\\0\le-1\end{cases}\) vô nghiệm
vậy \(m=-\frac{1}{9}\) là giá trị cần tìm
LM
27 tháng 2 2016
hệ :⇔{(m−3)x≤m+1(2m+1)≤2m⇔{(m−3)x≤m+1(2m+1)≤2m
suy ra hệ này có nghiệm duy nhất:
⇔m+1m−3=2m2m+1⇔⇔m+1m−3=2m2m+1⇔(m+1)(2m+1)=2m(m−3)(m+1)(2m+1)=2m(m−3)
⇔2m2+m+2m+1=2m2−6m⇔2m2+m+2m+1=2m2−6m
⇔m=−19∈(−12;3)⇔m=−19∈(−12;3)
nếu m=3m=3 thì hệ ⇔{0≤47x≤6⇔{0≤47x≤6có vô số nghiệm
nếu m=−12m=−12 thì hệ ⇔{−72x≤120≤−1⇔{−72x≤120≤−1 vô nghiệm
vậy m=−19m=−19 là giá trị cần tìm
25 tháng 1 2016
x4+(1−2m)x2+m2−1(1)
Đặt t=x2(t\(\ge\) 0) ta được:
t2+(1-2m)t+m2-1(2)
a)Để PT vô nghiệm thì:
\(\Delta=\left(1-2m\right)^2-4.1.\left(m^2-1\right)<0\)
<=>1-4m+4m2-4m2+4<0
<=>5-4m<0
<=>m>5/4
27 tháng 2 2016
giả sử : \(\frac{mx+m}{\left(m+1\right)x-m+2}>0\)\(,\text{∀}x\in\left[0;2\right]\)
\(\Rightarrow\frac{m.0+m}{\left(m+1\right).0-m+2}>0\) \(\Rightarrow\frac{m}{2-m}>0\)
\(\Rightarrow0\)\(<\)\(m<\)\(2\)
ngược lại \(0<\)\(m<2\) thì:
\(mx+m>0,\text{∀}x\in\left[0;2\right]\)
\(\left(m+1\right)x\ge0>m-2,\)\(\text{∀}x\in\left[0;2\right]\)
\(\Rightarrow\left(m+1\right)x-m+2>0,\text{∀}x\in\left[0;2\right]\)
\(\Rightarrow\frac{mx+m}{\left(m+1\right)x-m+2}>0,\text{∀}x\in\left[0;2\right]\)
vậy: \(0\)\(<\)\(m<\)\(2\) là kết quả cần tìm
CM
25 tháng 12 2018
Đáp án là B.
Đặt t = x - 2 x Đạo hàm t , = 1 + 2 x 2 > 0
Do đó t ( 1 ) ≤ t ≤ t ( 2 ) , ∀ x ∈ [ 1 ; 2 ] , suy ra - 1 ≤ t ≤ 1
Ta có x 2 + 4 x 2 = t 2 + 4 , x 4 + 16 x 4 = ( x 2 + 4 x 2 ) 2 - 8 = ( t 2 + 4 ) 2 - 8 = t 4 + 8 t 2 + 8
Phương trình đã cho trở thành
t 4 + 8 t 2 + 8 - 4 ( t 2 + 4 ) - 12 t = m ⇔ t 4 + 4 t 2 - 12 t = m + 8 ( * )
Phương trình đã cho có nghiệm trong đoạn [1;2] khi và chỉ khi phương trình (*) có nghiệm trong [-1;1] Xét hàm số y=f(t)= t 4 + 4 t 2 - 12 t trên [-1;1]
Đạo hàm y , = 4 t 8 + 8 t - 12 , t ∈ ( - 1 ; 1 ) . y , = 4 ( t - 1 ) ( t 2 + t + 3 ) < 0 , ∀ t ∈ ( - 1 ; 1 )
Bảng biến thiên:
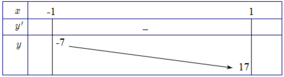
Do đó để phương trình đã cho có nghiệm trên [1;2] thì - 7 ≤ m + 8 ≤ 17 ⇔ - 15 ≤ m ≤ 9
CM
23 tháng 5 2017
Đáp án C
Ta có
f ' x = − m s i n x + 2 cos x − 3 ; y ' = 0 ⇔ − m s i n x + 2 cos x = 3
Phương trình này giải được với điều kiện là
m 2 + 2 2 ≥ 3 2 ⇔ m 2 ≥ 5 ⇔ m ∈ − ∞ ; − 5 ∪ 5 ; + ∞
