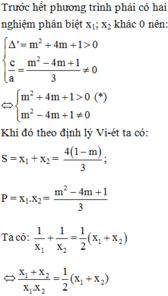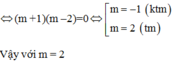LD
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
14 tháng 9 2021
\(a,x=-1\\ \Leftrightarrow1-2\left(m+1\right)+m^2-3m=0\\ \Leftrightarrow-1-5m+m^2=0\\ \Leftrightarrow m^2-5m-1=0\\ \Delta=25+4=29\\ \Leftrightarrow\left[{}\begin{matrix}m=\dfrac{5+\sqrt{29}}{2}\\m=\dfrac{5-\sqrt{29}}{2}\end{matrix}\right.\)
\(b,\)Pt có 2 nghiệm phân biệt
\(\Leftrightarrow\Delta=\left[2\left(m+1\right)\right]^2-4\left(m^2-3m\right)>0\\ \Leftrightarrow4m^2+8m+4-4m^2+12m>0\\ \Leftrightarrow20m+4>0\Leftrightarrow m>-\dfrac{1}{5}\)
\(c,\)Để pt có nghiệm duy nhất (nghiệm kép)
\(\Leftrightarrow\Delta=\left[2\left(m+1\right)\right]^2-4\left(m^2-3m\right)=0\\ \Leftrightarrow20m+4=0\\ \Leftrightarrow m=-\dfrac{1}{5}\)
PV
1
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 4 2021
\(\Delta'=9-m-3=6-m>0\Rightarrow m< 6\)
Theo hệ thức Viet: \(x_1+x_2=6\Rightarrow\dfrac{x_1+x_2}{2}=3\)
\(\Rightarrow\) Luôn tồn tại ít nhất 1 trong 2 giá trị \(x_1;x_2\) không nhỏ hơn 3
Nếu \(x_2\ge3\Rightarrow\left|x_1-1\right|+3x_2\ge3x_2\ge9\)
Dấu "=" xảy ra khi và chỉ khi \(\left\{{}\begin{matrix}x_1-1=0\\x_2=3\end{matrix}\right.\) \(\Rightarrow x_1+x_2=4\) (ktm)
\(\Rightarrow x_2< 3\) và \(x_1\ge3\Rightarrow\left|x_1-1\right|=x_1-1\)
Do đó:
\(x_1-1+3x_2=9\Rightarrow x_1=10-3x_2\)
Thế vào \(x_1+x_2=6\Rightarrow10-2x_2=6\Rightarrow x_2=2\Rightarrow x_1=4\)
\(x_1x_2=m+3\Rightarrow m+3=8\Rightarrow m=5\)
12 tháng 5 2023
Δ=(m^2+3)^2-4(2m^2+2)
=m^4+6m^2+9-8m^2-8
=m^4-2m^2+1=(m^2-1)^2
Để phương trình có hai nghiệm phân biệt thì m^2-1<>0
=>m<>1 và m<>-1
1
TK
11 tháng 5 2021
\(\left(m+1\right)\cdot x^2+5x+m^2-1=0\)
\(\Delta=5^2-4\cdot\left(m+1\right)\left(m^2-1\right)\)
\(\Delta=25-4\cdot\left(m^3-m+m^2-1\right)\)
\(\Delta=-4m^3-4m^2+4m+29\)
\(\Delta=-4m\left(m^2+m-1\right)+29\)
\(\Delta=-4m[\left(m+\dfrac{1}{2}\right)^2-\dfrac{5}{4}]+29\)
\(\Delta=-4m\left(m+\dfrac{1}{2}\right)^2+34\)
Vì \(\left(m+\dfrac{1}{2}\right)^2\ge0\) và 34>0
Nên để phương trình có 2 nghiệm phân biệt
Thì \(-4m\ge0\)
⇔\(m\le0\)
Vậy m≤0
NA
1
KV
30 tháng 5 2023
a) m = 1, phương trình tương đương:
x² + 4x = 0
⇔ x(x + 4) = 0
⇔ x = 0 hoặc x + 4 = 0
*) x + 4 = 0
⇔ x = -4
Vậy S = {-4; 0}
b) ∆' = [-(m - 3)]² - (m² - 1)
= m² - 6m + 9 - m² + 1
= -6m + 10
Phương trình có hai nghiệm phân biệt khi ∆' > 0
⇔ -6m + 10 > 0
⇔ -6m > -10
⇔ m < 5/3
Vậy m < 5/3 thì phương trình đã cho có hai nghiệm phân biệt
