Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
\(4x^3-6x^2+m=0\Leftrightarrow4x^3-6x^2=-m\)
Xét hàm \(f\left(x\right)=4x^3-6x^2\)
\(f'\left(x\right)=12x^2-12x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
BBT:
Từ BBT ta thấy đường thẳng \(y=-m\) cắt \(y=4x^3-6x^2\) tại 3 điểm pb khi:
\(-2< -m< 0\Leftrightarrow0< m< 2\)
2.
Pt hoành độ giao điểm:
\(\dfrac{x-3}{x+1}=x+m\)
\(\Rightarrow x-3=\left(x+m\right)\left(x+1\right)\)
\(\Leftrightarrow x^2+mx+m+3=0\) (1)
Đường thẳng cắt đồ thị tại 2 điểm pb khi và chỉ khi (1) có 2 nghiệm pb
\(\Leftrightarrow\Delta=m^2-4\left(m+3\right)>0\)
\(\Rightarrow\left[{}\begin{matrix}m>6\\m< -2\end{matrix}\right.\)

phương trình hoành độ giao điểm
\(-x^3+3x^2-2=m(2-x)+2\Leftrightarrow (x-2)(x^2-x-2-m)=0\)
Vậy \(x_B, x_C\) là nghiệm của phương trình $x^2-x-2-m=0$.
Điều kiện có nghiệm: $\Delta=4m+9>0\Leftrightarrow m>-\dfrac{9}{4}$
Mặt khác, theo Định lý Viet thì \(\begin{cases} x_B+x_C=1\\ x_Bx_C=-2-m \end{cases}\)
Lại có \(y'=-3x^2+6x=3x(2-x)\) nên tích hệ số góc của tiếp tuyến tại B và C là
\(y'(x_B)y'(x_C)=9x_Bx_C(2-x_B)(2-x_C)=9x_Bx_C[4-2(x_B+x_C)+x_Bx_C]\)
Do đó \(y'(x_B)y'(x_C)=9(-2-m)(4-2-2-m)=9(m^2+2m)=9[(m+1)^2-1]\geq -9\)
Vậy giá trị nhỏ nhất của tích hai hệ số góc của tiếp tuyến tại B và C là -9 khi m=-1



Bạn coi lại đề, với đề này thì \(m\in\left(a;1\right)\) trong đó a là 1 nghiệm xấu của pt bậc 3 (ko giải được với chương trình phổ thông)
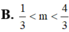
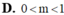
Chọn D