Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt ![]()
Suy ra ![]()
Ta có ![]()
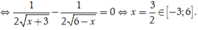
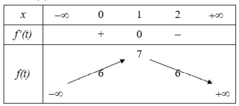
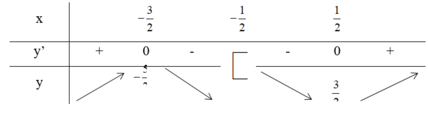
Ta có bảng biến thiên
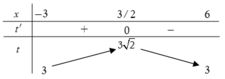
Từ bảng biến thiên ta suy ra ![]()
Khi đó bất phương trình trở thành: ![]()
![]()
Xét hàm số ![]() với
với ![]()
Ta có ![]()
Suy ra hàm số f(t) nghịch biến trên ![]()
![]()
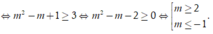
Chọn C.

x4+(1−2m)x2+m2−1(1)
Đặt t=x2(t\(\ge\) 0) ta được:
t2+(1-2m)t+m2-1(2)
a)Để PT vô nghiệm thì:
\(\Delta=\left(1-2m\right)^2-4.1.\left(m^2-1\right)<0\)
<=>1-4m+4m2-4m2+4<0
<=>5-4m<0
<=>m>5/4

Đáp án A
Phương pháp: Chia cả 2 vế cho 3x, đặt  , tìm điều kiện của t.
, tìm điều kiện của t.
Đưa về bất phương trình dạng ![]()
Cách giải :
![]()

Ta có 

Đặt  , khi đó phương trình trở thành
, khi đó phương trình trở thành
![]()

![]()
![]()
![]()
![]()
Ta có: 



Vậy 

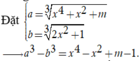
Khi đó bất phương trình trở thành
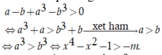
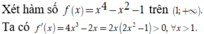
Suy ra hàm số f(x) đồng biến trên ![]()
Do đó yêu cầu bài toán ![]()
Chọn B.



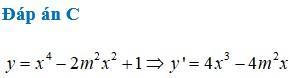
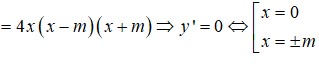
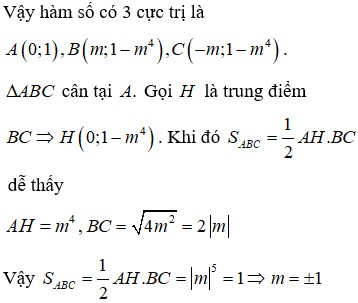

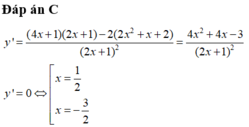
Đáp án B
Bất PT: x − x − 1 < m ⇔ x − 1 − x − 1 − m − 1 < 0
Đặt t = x − 1 t ≥ 0 ta được BPT t 2 − t − m − 1 < 0 1 ;
Như vậy bài toán trở thành tìm để BPT (1) có nghiệm t ≥ 0
⇒ Δ = 1 + 4 m − 1 = 4 m − 3 > 0 ⇔ m > 3 4 t 2 = 1 + 4 m − 3 2 > 0 ⇔ m > 3 4
Như vậy ta chọn đáp án B do 3 4 < 1