T
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TL
1
OD
22 tháng 6 2017
Gọi d là ƯCLN (2n +2 và 2n -4)
Ta có: 2n- 4 =2n + 2- 6 \(⋮\)
2n + 2\(⋮\)
\(\Rightarrow\)(2n +2 -6) - (2n +2)
= 2n +2 - 6 -2n -2 =2n -2n +2 - 6- 2
=0+2 - 6 -2 = -6 \(⋮\)d
\(\Rightarrow\)d \(\in\) Ư ( 6) = (1, -1 , 2, -2 , 3, -3 ,6, -6)
\(\Rightarrow\)2n +2 và 2n -4 \(⋮\)các Ư của 6 (như trên).
\(\Rightarrow\)2n + 2 và 2n-4 không ng tố cùng nhau vói mọi số n
Vậy n\(\in\)rỗng
29 tháng 12 2015
a)Vì hai số tự nhiên liên tiếp có UC là 1 nên =>Hai số tự nhiên lien tiếp khác 0 là hai số nguyên tố cùng nhau
b)Vì hai số tự nhiên liên tiếp có UC là 1 nên =>Hai số tự nhiên lien tiếp là hai số nguyên tố cùng nhau
tick nha
NT
1
NM
Nguyễn Minh Quang
Giáo viên
23 tháng 11 2020
gọi a là ước chung lớn nhất của 2n+1 và 3n+2
do đó a phải là ước của \(2\left(3n+2\right)-3\left(2n+1\right)=1\) do đó a=1
hay 2n+1 và 3n+2 là hai số nguyên tố cùng nhau.
b.gọi b là ước chung lớn nhất của 2n+3 và 4n+5
do đó b phải là ước của \(2\left(2n+3\right)-\left(4n+5\right)=1\)do đó b=1
hay 2n+3 và 4n+5 là hai số nguyên tố cùng nhau
CM
17 tháng 4 2017
a, Gọi d ∈ ƯC(n,n+1) => (n+1) – 1 ⋮ d => 1 ⋮ d => d = 1. Vậy n, n+1 là hai số nguyên tố cùng nhau
b, Gọi d ∈ ƯC(2n+1,2n+3) => (2n+3) – (2n+1) ⋮ d => 2 ⋮ d => d ∈ {1;2}. Vì d là số lẻ => d = 1 => dpcm
c, Gọi d ∈ ƯC(2n+1,3n+1) => 3.(2n+1) – 2.(3n+1) ⋮ d => 1 ⋮ d => d = 1 => dpcm
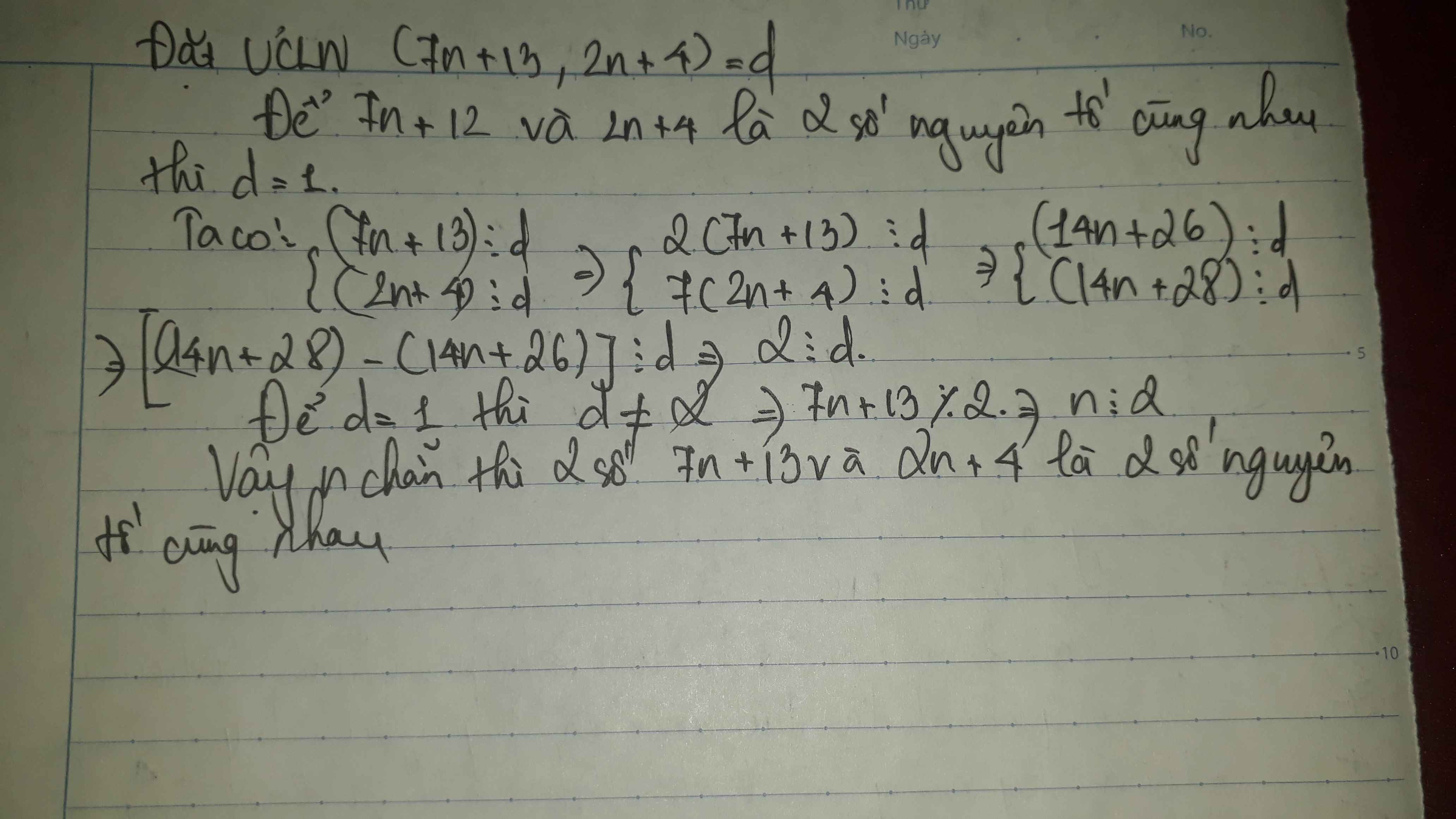
Vì 2n+3 và 2n+4 là 2 số liên tiếp. Mà các chữ số liên tiếp đều là 2 số nguyên tố cùng nhau.
Suy ra (2n+3;2n+4)=1 (điều phải chứng minh)
kik mình nha