Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọihai số cần tìm lần lượt là a,b
Theo đề, ta có: a+b=84 và a=6b+7
=>a+b=84 và a-6b=7
=>a=73 và b=11

Gọi số bé là xx thì số lớn là 156−x156−x . Theo đề bài ta có
156−x=6x+9⇔7x=147⇔x=21

Gọi số lớn là x, số nhỏ là y (x, y ∈ N*); x,y > 124.
Tổng hai số bằng 1006 nên ta có: x + y = 1006
Số lớn chia số nhỏ được thương là 2, số dư là 124 nên ta có: x = 2y + 124.
Ta có hệ phương trình:
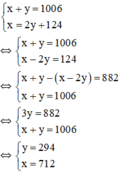
Vậy hai số tự nhiên phải tìm là 712 và 294.
Chú ý : Số bị chia = số chia. thương + số dư

Gọi số lớn là x, số nhỏ là y (x, y ∈ N*); x,y > 124.
Tổng hai số bằng 1006 nên ta có: x + y = 1006
Số lớn chia số nhỏ được thương là 2, số dư là 124 nên ta có: x = 2y + 124.
Ta có hệ phương trình:
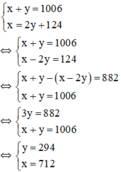
Vậy hai số tự nhiên phải tìm là 712 và 294.
Chú ý : Số bị chia = số chia. thương + số dư
Kiến thức áp dụng
Giải bài toán bằng cách lập hệ phương trình:
Bước 1: Lập hệ phương trình
- Chọn các ẩn số và đặt điều kiện thích hợp
- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn
- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.
- Từ các phương trình vừa lập rút ra được hệ phương trình.
Bước 2: Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).
Bước 3: Đối chiếu nghiệm với điều kiện và kết luận.

gọi số lớn là x số nhỏ là y(2014>x>y>0)
ta có x+y=2014 và x=y+14<=>x-y=14
ta được bài toán tìm ẩn biết tổng và hiệu của chúng
=>x=(2014+14):2=1014(nhận)
=>y=2014-1014=1000(nhận)
vậy 2 số đó là 1014 và 1000

Gọi x là số lớn, y là số bé. ĐK : x>y và 0<x,y<1006
Vì tổng của 2 số này bằng 1006 nên : x+y=1006 (*)
Mà nếu lấy số lớn chia cho số nhỏ thì đc thương là 2 và số dư là 124 nên ta có: x= 2y + 124 .
Thay vào (*) ta đc: y+2y+124 =1006<=>3y = 882=>y=882/3 = 294
=>x=1006-294 =712
Vậy....................
Gọi số lớn là x , số nhỏ là y ( x , y ∈ N* ) ; x > 124.
Vì tổng hai số bằng 1006 nên ta có: x + y = 1006 .
Số lớn chia số nhỏ được thương là 2, số dư là 124 nên ta có: x = 2y + 124.
Ta có hệ phương trình:
Vậy ..........

Gọi số lớn là x, số nhỏ là y \(\left(x,y\inℕ^∗\right);x,y>124\)
Tổng hai số bằng 1006 nên ta có: x + y = 1006
Số lớn chia số nhỏ được thương là 2, số dư là 124 nên ta có: x = 2y + 124.
Ta có hệ phương trình :
\(\hept{\begin{cases}x+y=1006\\x=2y+124\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x+y=1006\\x-2y=124\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x+y-\left(x-2y\right)=882\\x+y=1006\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}3y=882\\x+y=1006\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=294\\x=712\end{cases}}\)
Vậy hai số tự nhiên phải tìm là 712 và 294

Gọi số lớn là x, số nhỏ là y (a, y ∈ N*); x > 124. Ta có: Tổng bằng 1006 nên được: x + y = 1006
Số lớn chia số nhỏ được thương là 2, số dư là 124 nên ta có điều kiện là y > 124 và có phương trình: x = 2y + 124
Ta có hệ phương trình:
Vậy hai số tự nhiên phải tìm là 712 và 294.
Nếu lấy số lớn chia cho số bé thì được 2 dư 124 => Số lớn gấp số bé 2 lần và 124 đơn vị .
=> Số bé là :
( 1006 - 124 ) : ( 2 + 1 ) = 294
Số lớn là :
294 x 2 + 124 = 712
Đáp số : 712 và 294

neu chia ko du thi tong la :
156 - 9 =147
ta co so do :
so be : --------
so lon : --------/---------/--------/--------/--------/--------/
so lon la :
147 : ( 6 +1 ) x 6 = 126
so be la :
147 - 126 = 21
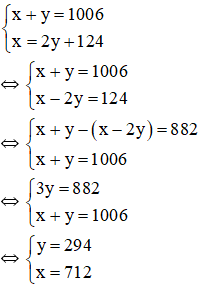
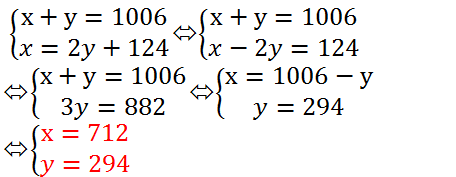
Gọi hai số cần tìm lần lượt là a,b
Theo đề, ta có: a+b=84 và a=6b+7
=>a+b=84 và a-6b=7
=>a=73 và b=11