Tìm hai số biết rằng 4 lần số thứ hai cộng với 5 lần số thứ nhất bằng 18040, và 3 lần số thứ nhất hơn 2 lần số thứ hai l...

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

MT

Mai's tồ's

10 tháng 2 2019

Tìm hai số biết rằng 4 lần số thứ hai cộng với 5 lần số thứ nhất bằng 18040, và 3 lần số thứ nhất hơn 2 lần số thứ hai là 2002.

Giải hệ phương trình nha

1

TT

Trần Thùy Linh

1 tháng 4 2020

https://i.imgur.com/GhY2A88.jpg

Các câu hỏi dưới đây có thể giống với câu hỏi trên

LK

le khanh huy

8 tháng 2 2017 - olm

tìm hai số biết rằng bốn lần số thứ 2 cộng với 5 lần số thứ nhát bằng 18040 và 3 lần số thứ nhất hơn hai lần số thứ hai là 2002

0

PT

phạm thanh nga

14 tháng 1 2020 - olm

GIẢI BÀI TOÁN BẰNG CÁCH LẬP HỆ PHƯƠNG TRÌNHa,Tìm hai số biết rằng 4 lần số thứ hai cộng với 5 lần số thứ nhất =18040, và 3 lần số thứ nhất hơn 2 lần số thứ hai là 2002. b,Tìm một số tự nhiên có hai chữ số, biết rằng số đó gấp 4 lần tổng các chữ số của nó. Nếu viết hai chữ số của nó theo thứ tự ngược lạ thì được số mới lơn hơn số ban đầu 36 đơn...

1

NE

$๖ۣۜN๖ۣۜE๖ۣۜV ๖ۣۜE ๖ۣۜR $ ^^๖ۣۜG๖ۣۜ...

14 tháng 1 2020

a)Gọi 2 số cần tìm là a và b lần lượt là số t1 và t2 , ta có hpt :

5a+4b=18040

3a-2b=2002

giải hpt ta được a=2004;b=2005

b) Gọi số tự nhiên cần tim là ab (nhớ gạch ở trên ab đó) ;(a;b thuộc N;0<a"<9;0<b'<9)

theo đề bài ta có :

ab=4(a+b)

ba-ab=36

=>a=4;b=8 hay ab=48

nhớ các chữ ab hay ba có gạch ở trên đầu đó

PT

phạm thanh nga

13 tháng 1 2020 - olm

GIẢI BÀI TOÁN BẰNG CÁCH LẬP HỆ PHƯƠNG TRÌNHa,Tìm hai số biết rằng 4 lần số thứ hai cộng với 5 lần số thứ nhất =18040, và 3 lần số thứ nhất hơn 2 lần số thứ hai là 2002. b,Tìm một số tự nhiên có hai chữ số, biết rằng số đó gấp 4 lần tổng các chữ số của nó. Nếu viết hai chữ số của nó theo thứ tự ngược lạ thì được số mới lơn hơn số ban đầu 36 đơn...

0

AA

Admin (a@olm.vn)

Admin VIP

22 tháng 3 2021 - olm

Tìm hai số biết rằng bốn lần số thứ nhất cộng với năm lần số thứ hai bằng 2142 và sáu lần số thứ hai hơn 4 lần số thứ nhất là 960.

0

AL

ARMY love BTS

2 tháng 4 2020

Giải bài toán bằng cách lập hệ phương trình :

Tìm hai số biết rằng hai lần số thứ nhất cộng với 3 lần số thứ hai bằng 10098 cho bốn lần số thứ nhất hơn ba lần số thứ hai là 2016

1

TT

Trần Thùy Linh

2 tháng 4 2020

https://i.imgur.com/iLqM6tL.jpg

NH

Nguyễn Hằng

18 tháng 4 2021

Tìm hai số biết rằng 2 lần số thứ nhất lớn hơn 3 lần số thứ hai là 9 và hiôu các bình phương của chúng bằng119

1

AH

Akai Haruma

Giáo viên

20 tháng 4 2021

Lời giải:

Gọi hai số cần tìm là $a$ và $b$. Theo bài ra ta có:
\(\left\{\begin{matrix} 2a-3b=9\\ a^2-b^2=119\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2a=3b+9\\ (2a)^2-(2b)^2=476\end{matrix}\right.\)

\(\Rightarrow (3b+9)^2-4b^2=476\)

\(\Leftrightarrow 5b^2+54b-395=0\)

$\Leftrightarrow (b-5)(5b+79)=0$

$\Rightarrow b=5$ hoặc $b=-\frac{79}{5}$

Với $b=5$ thì $a=\frac{3b+9}{2}=12$

Với $b=\frac{-79}{5}$ thì $a=\frac{3b+9}{2}=\frac{-96}{5}$

PT

Pham Trong Bach

7 tháng 2 2019

Cho hai số tự nhiên biết rằng hai lần số thứ nhất hơn ba lần số thứ hai là 9 và hiệu các bình phương của chúng bằng 119. Tìm số lớn hơn.

A. 12

B. 13

C. 32

D. 33

1

CM

Cao Minh Tâm

7 tháng 2 2019

Đáp án A

Gọi số thứ nhất là a; a ∈ N, số thứ hai là b; b ∈ N Vì hai lần số thứ nhất hơn ba lần số thứ hai là 9 nên ta có:

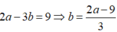
Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

Vì hiệu các bình phương của chúng bằng 119 nên ta có phương trình:

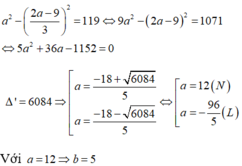
Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

Vậy số lớn hơn là 12.

PT

Pham Trong Bach

2 tháng 8 2017

Cho hai số tự nhiên biết rằng hai lần số thứ nhất hơn ba lần số thứ hai là 9 và hiệu các bình phương của chúng bằng 119. Tìm số lớn hơn.

A. 12

B. 13

C. 32

D. 33

1

CM

Cao Minh Tâm

2 tháng 8 2017

Đáp án A