Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ace Legona làm chi tiết cho em với em cũng thử rồi nhưng ko được

\(A=\left(x-1\right)\left(x-8\right)\left(x-4\right)\left(x-5\right)+2002\)
\(\Leftrightarrow A=\left(x^2-9x+8\right)\left(x^2-9x+20\right)+2002\)
Đặt \(x^2-9x+14=y\)
\(\Rightarrow A=\left(y-6\right)\left(y+6\right)+2002\)
\(\Leftrightarrow A=y^2-36+2002\)
\(\Leftrightarrow A=y^2+1966\ge1966\)
Dấu "=" xảy ra khi
\(x^2-9x+14=0\)
\(\Leftrightarrow x=2,7\)

Bạn kiểm tra lại đề, \(f\left(x\right)=\dfrac{x^3}{1-3x-3x^2}\) hay \(f\left(x\right)=\dfrac{x^3}{1-3x+3x^2}\)

a) \(B=-3x^2-4x+1\)
\(B=-\left(3x^2+4x-1\right)\)
\(B=-\left[\sqrt{3}x+2.\sqrt{3}x.+\dfrac{2\sqrt{3}}{3}+\left(\dfrac{2\sqrt{3}}{3}\right)^2-\left(\dfrac{2\sqrt{3}}{3}\right)^2-1\right]\)
\(B=-\left(\sqrt{3}x+\dfrac{2\sqrt{3}}{3}\right)^2+\dfrac{7}{3}\le\dfrac{7}{3}\)
\(Max_B=\dfrac{7}{3}\) khi \(x=\dfrac{-2}{3}\)
b) \(C\left(x\right)=x^4-10x^3+26x^2-10x+30\)
\(=\left(x^2\right)^2-2.x^2.5x+\left(5x\right)^2+x^2-2.x.5+5^2+5\)
\(=\left(x^2-5x\right)^2+\left(x-5\right)^2+5\)
\(C\left(y\right)=\left(y+1\right)\left(y+2\right)\left(y+3\right)\left(y+4\right)\)
Nhóm (y+1)(y+4)=t
Nhóm (y+2)(y+3)=t+2
Xong tìm Min được liền
c) Min=2010
d) Viết đề thiếu dấu, có vấn đề, xem lại
e) C= -[(x-y)2+2(x-y).7+72+x2-2.x.2+22-1945]
Xong tìm được Max

Lời giải:
$G=1-\sqrt{(3x-1)^2}+(3x-1)^2=1-|3x-1|+|3x-1|^2$
Đặt $|3x-1|=a$ với $a\geq 0$
Ta cần tìm GTNN của $G=1-a+a^2$
Có: $G=(a-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$ với mọi $a\geq 0$
Do đó gtnn của $G$ là $\frac{3}{4}$

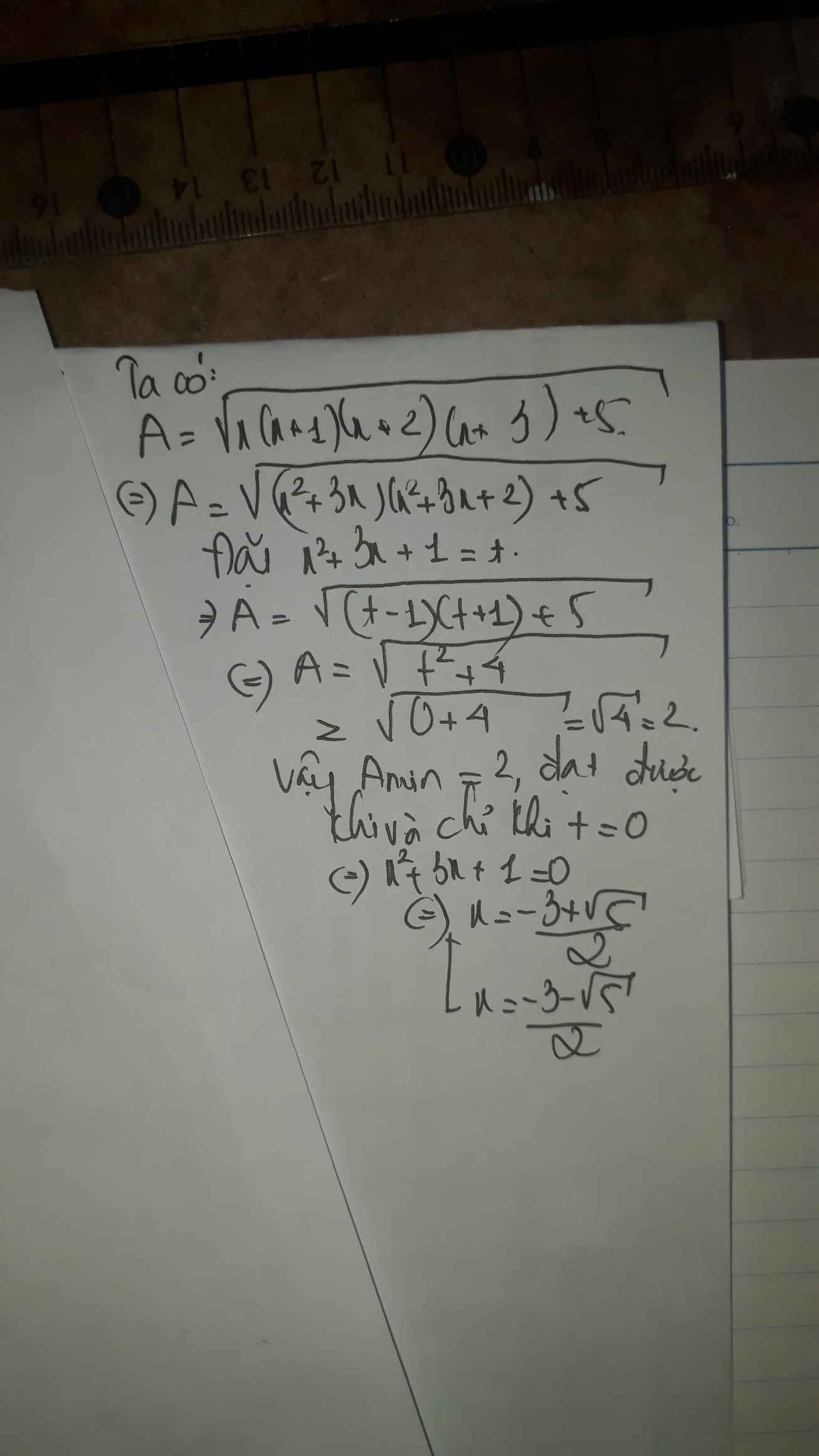
Cái này bỏ nha
Cái này e ko bt sai hay đúng thấy mấy a cj giải vậy á