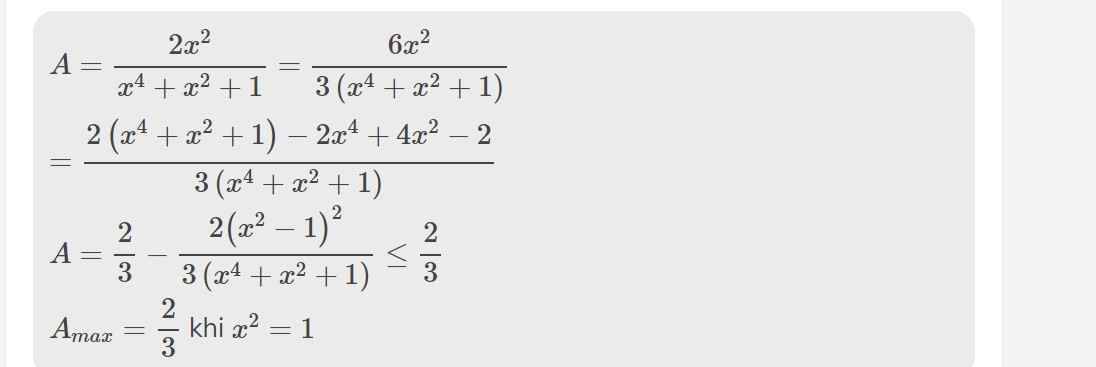I
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
1 tháng 4 2020
Bài 2 bạn tham khảo cách làm của cô Linh Chi tại đây nhé :
Câu hỏi của nguyen trung nghia - Toán lớp 8 - Học toán với OnlineMath
Học tốt và cá tháng tư đừng để bị troll nha !!!!!!!!!!!
1 tháng 4 2020
B1:
\(M=\left(x+y\right)\left(\frac{1}{x}+\frac{1}{y}\right)\)
\(=2+\frac{x}{y}+\frac{y}{x}\)
Nhờ dự đoán được điểm rơi,ta chứng minh bất đẳng thức sau luôn đúng:\(\frac{x}{y}+\frac{y}{x}\le\frac{5}{2}\)
Thật vậy !!!
\(\frac{x}{y}+\frac{y}{x}\le\frac{5}{2}\)
\(\Leftrightarrow\left(\frac{x}{y}-\frac{1}{2}\right)+\left(\frac{y}{x}-2\right)\le0\)
\(\Leftrightarrow\frac{2x-y}{2y}+\frac{y-2x}{x}\le0\)
\(\Leftrightarrow\frac{2x^2-xy+2y^2-4xy}{2xy}\le0\)
\(\Leftrightarrow2x^2-5xy+2y^2\le0\)
\(\Leftrightarrow\left(x-2y\right)\left(2x-y\right)\le0\) ( đúng )
Dấu "=" xảy ra tại \(x=1;y=2\)
Vậy \(M_{max}=\frac{9}{2}\Leftrightarrow x=1;y=2\)
10 tháng 3 2020
\(\frac{x+2}{x+3}-\frac{x+1}{x-1}=\frac{4}{\left(x-1\right)\left(x+3\right)}\left(x\ne-3;x\ne1\right)\)
\(\Leftrightarrow\frac{x+2}{x+3}-\frac{x+1}{x-1}-\frac{4}{\left(x-1\right)\left(x+3\right)}=0\)
\(\Leftrightarrow\frac{\left(x+2\right)\left(x-1\right)}{\left(x+3\right)\left(x-1\right)}-\frac{\left(x+1\right)\left(x+3\right)}{\left(x-1\right)\left(x+3\right)}-\frac{4}{\left(x-1\right)\left(x+3\right)}=0\)
\(\Leftrightarrow\frac{x^2+x-2}{\left(x+3\right)\left(x-1\right)}-\frac{x^2+4x+3}{\left(x-1\right)\left(x+3\right)}-\frac{4}{\left(x-1\right)\left(x+3\right)}=0\)
\(\Leftrightarrow\frac{x^2+x-2-x^2-4x-3-4}{\left(x-1\right)\left(x+3\right)}=0\)
\(\Leftrightarrow\frac{-3x-9}{\left(x-1\right)\left(x+3\right)}=0\)
\(\Leftrightarrow\frac{-3\left(x+3\right)}{\left(x-1\right)\left(x+3\right)}=0\)
\(\Leftrightarrow\frac{-3}{x-1}=0\)
=> PT vô nghiệm
12 tháng 1 2023
a: ĐKXĐ: x<>1; x<>2; x<>3
\(K=\left(\dfrac{x^2}{\left(x-2\right)\left(x-3\right)}+\dfrac{x^2}{\left(x-1\right)\left(x-2\right)}\right)\cdot\dfrac{\left(x-1\right)\left(x-3\right)}{x^4+2x^2+1-x^2}\)
\(=\dfrac{x^3-x^2+x^3-3x^2}{\left(x-2\right)\left(x-3\right)\left(x-1\right)}\cdot\dfrac{\left(x-1\right)\left(x-3\right)}{\left(x^2+1+x\right)\left(x^2+1-x\right)}\)
\(=\dfrac{2x^3-4x^2}{\left(x-2\right)}\cdot\dfrac{1}{\left(x^2+x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{2x^2\left(x-2\right)}{\left(x-2\right)\left(x^4+x^2+1\right)}=\dfrac{2x^2}{x^4+x^2+1}\)
b:
SN
0
