VT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TA
14 tháng 5 2016
Đặt \(t=\sin^2x\Rightarrow\begin{cases}\cos^2x=1-t\\t\in\left[0;1\right]\end{cases}\) \(\Leftrightarrow f\left(x\right)=5^t+5^{1-t}=g\left(t\right);t\in\left[0;1\right]\)
Ta có : \(g'\left(t\right)=5^t\ln5-5^{1-t}\ln5=\left(5^t-5^{1-t}\right)\ln5=0\)
\(\Leftrightarrow5^t=5^{1-t}\)
\(\Leftrightarrow t=1-t\)
\(t=\frac{1}{2}\)
Mà \(\lim\limits_{x\rightarrow-\infty}g\left(t\right)=\lim\limits_{x\rightarrow-\infty}\left(5^t-5^{1-t}\right)=+\infty\)
\(\lim\limits_{x\rightarrow+\infty}g\left(t\right)=\lim\limits_{x\rightarrow+\infty}\left(5^t-5^{1-t}\right)=+\infty\)
Ta có bảng biến thiên
\(\Rightarrow\) Min \(f\left(x\right)=2\sqrt{5}\) khi \(t=\frac{1}{2}\Leftrightarrow\sin^2x=\frac{1}{2}\Leftrightarrow\frac{1-\cos2x}{2}=\frac{1}{2}\)
\(\Leftrightarrow\cos2x=0\)
\(\Leftrightarrow x=\frac{\pi}{4}+\frac{k\pi}{2}\) \(\left(k\in Z\right)\)
TA
14 tháng 5 2016
\(0\le\sin^2x\le1\Rightarrow0,5^0\ge0,5^{\sin^2x}\ge0,5^1\)
\(\Leftrightarrow1\ge f\left(x\right)\ge\frac{1}{2}\)
\(\Leftrightarrow\) Max f(x) = 1 khi \(x=k\pi\)
Min f(x) =\(\frac{1}{2}\) khi \(x=\frac{\pi}{2}+k\pi\) \(k\in Z\)
14 tháng 5 2016
Đặt \(t=\sin^2x\) với \(t\in\left[0;1\right]\Rightarrow f\left(x\right)=0,5^t=g\left(t\right)\) với \(t\in\left[0;1\right]\)
Ta có : \(g'\left(t\right)=0,5^1\ln0,5=-0,5^t\ln2< 0\) với mọi \(t\in\left[0;1\right]\) hàm số nghịch biến với mọi \(t\in\left[0;1\right]\)
\(\Rightarrow0\le t\le1\Rightarrow g\left(0\right)\ge g\left(t\right)\ge g\left(1\right)\Leftrightarrow1\ge g\left(t\right)\ge\frac{1}{2}\)
Vậy Max f(x) = 1 khi \(x=k\pi\)
Min \(f\left(x\right)=\frac{1}{2}\) khi \(x=\frac{\pi}{2}+k\pi\) (k thuộc Z)
BN
1
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 12 2021
\(y'=6x^2+6x-12=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
\(y\left(-1\right)=14\) ; \(y\left(1\right)=-6\) ; \(y\left(5\right)=266\)
\(\Rightarrow\min\limits_{\left[-1;5\right]}y=-6\) ; \(\max\limits_{\left[-1;5\right]}y=266\)
CM
15 tháng 9 2018
y = x 2 + 2 x + m - 4 = ( x + 1 ) 2 + m - 5
Ta có ( x + 1 ) 2 + m - 5 ∈ m - 5 ; m - 1
Giá trị lớn nhất của hàm số y = x 2 + 2 x + m - 4 trên đoạn[ -2; 1] đạt giá trị nhỏ nhất khi
m - 5 < 0 m - 1 > 0 5 - m = m - 1 ⇔ m = 3
Chọn B.
PT
1
CM
4 tháng 3 2018
Trên đoạn [-1; 1], ta có :
y = log 5 x
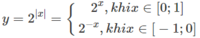
Do đó, trên đoạn [0;1] hàm số đồng biến, trên đoạn [-1;0] hàm số nghịch biến. Suy ra các giá trị lớn nhất và giá trị nhỏ nhất sẽ đạt được tại các đầu mút.
Ta có: y(−1) = 2 - - 1 = 2 1 = 2, y(0) = 2 0 = 1, y(1) = 2 1 = 2
Vậy max y = y(1) = y(−1) = 2, min y = y(0) = 1.
PT
1
CM
16 tháng 9 2019
Trên đoạn [-1; 1], ta có :
y = log 5 x
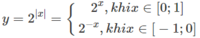
Do đó, trên đoạn [0;1] hàm số đồng biến, trên đoạn [-1;0] hàm số nghịch biến. Suy ra các giá trị lớn nhất và giá trị nhỏ nhất sẽ đạt được tại các đầu mút.
Ta có: y(−1) = 2 - ( - 1 ) = 2 1 = 2, y(0) = 2 0 = 1, y(1) = 2 1 = 2
Vậy max y = y(1) = y(−1) = 2, min y = y(0) = 1.
CM
25 tháng 1 2019
Chọn A
Đặt 
ta có 
với 
=> hàm số đồng biến trên [-1;1]
Vậy M + 2019m = 2
Nên chọn A.
