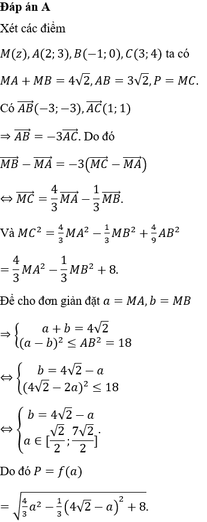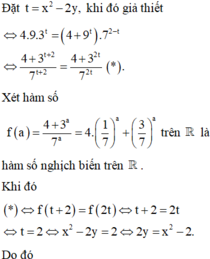TQ
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TN
3
26 tháng 4 2016
A=(x+1)*(x+2)*(x+3)*(x+4)
Ta có (x+1);(x+2);(x+3) và (x+4) sẽ xảy ra các trường hợp sau
Th1:(x+1);(x+2);(x+3) và (x+4) đều là số âm
Nên tích (x+1)*(x+2)*(x+3)*(x+4) sẽ là số dương
Hay (x+1)*(x+2)*(x+3)*(x+4)>0
Th2:1 trong các số (x+1);(x+2);(x+3);(x+4) sẽ=0
Nên (x+1)*(x+2)*(x+3)*(x+4)=0
Th2:các số (x+1);(x+2);(x+3);(x+4) đều là số dương
Nên (x+1)*(x+2)*(x+3)*(x+4)>0
Trong các trường hợp trên thì ta thấy trường hợp có GTNN là th2 nên biểu thức A sẽ có giá trị nhỏ nhất là 0(tick nha)
CM
1 tháng 1 2020
Ta có x + y = 2 ⇒ y = 2 - x ≥ 0 ⇒ 0 ≤ x ≤ 2 . Thay y = 2 - x và biểu thức P ta được
P = 1 3 x 3 + x 2 + 2 - x 2 - x + 1 = 1 3 x 3 + 2 x 2 - 5 x + 5 = f x
với x ∈ 0 ; 2
Đạo hàm f ' x = x 2 + 4 x - 5 = 0 ⇔ x = 1 x = - 5
Do x ∈ 0 ; 2 nên loại x = -5
f 1 = 7 3 ; f 0 = 5 ; f 2 = 17 3
Vậy m i n x ∈ 0 ; 2 P = m i n x ∈ 0 ; 2 f x = 7 3 khi và chỉ khi x = 1
Đáp án B
CM
17 tháng 4 2017
Đáp án C.
Ta có:
G T ⇔ 5 x + 2 y + x + 2 y − 3 − x − 2 y = 5 x y − 1 − 3 1 − x y + x y − 1.
Xét hàm số
f t = 5 t + t − 3 − t ⇒ f t = 5 t ln 5 + 1 + 3 − t ln 3 > 0 ∀ t ∈ ℝ
Do đó hàm số đồng biến trên ℝ suy ra f x + 2 y = f x y − 1 ⇔ x + 2 y = x y − 1
⇔ x = 2 y + 1 y − 1 ⇒ T = 2 y + 1 y − 1 + y . Do x > 0 ⇒ y > 1
Ta có: T = 2 + y + 3 y − 1 = 3 + y − 1 + 3 y − 1 ≥ 3 + 2 3 .
NT
5
10 tháng 12 2017
Ta có : H = |x - 3| - |4 + x| \(\ge\left|x-3-4-x\right|=-7\)
Vậy GTNN của biểu thức là -7
CC
0
