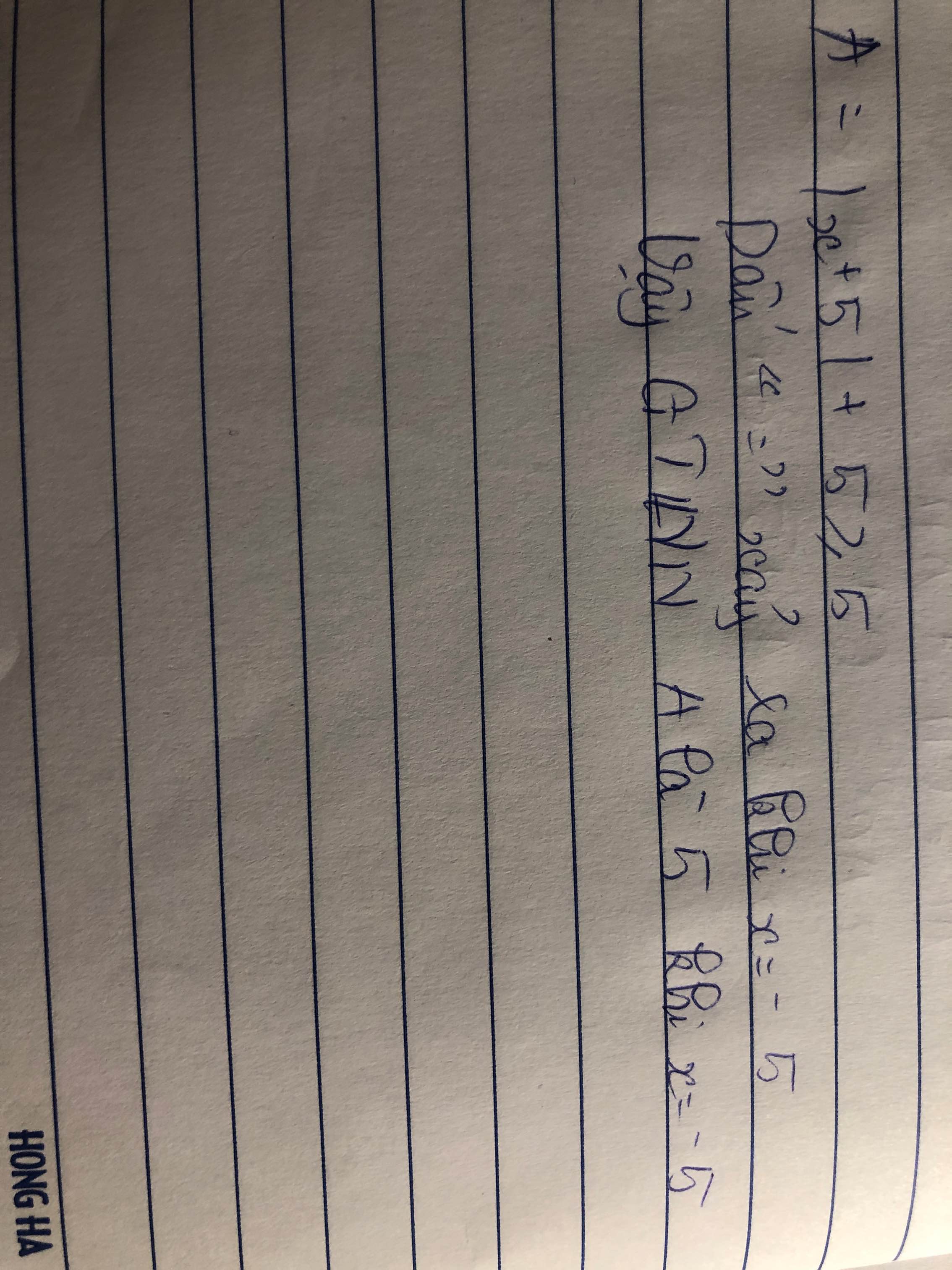Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left|x+1,5\right|\ge0\forall x\)
Dấu " = " xảy ra khi
| x + 1,5 | = 0
x = -1,5
Vậy MinA = 0 <=> x = -1,5
b)
\(\left|x-2\right|\ge0\forall x\Rightarrow\left|x-2\right|-\frac{9}{10}\ge\frac{9}{10}\forall x\)
Dấu " = " xảy ra khi
| x - 2 | = 0
x = 2
Vậy MinA = \(\frac{9}{10}\)<=> x = 2
\(-\left|2x-1\right|\le0\forall x\)
Dấu " = " xảy ra khi :
- | 2x - 1 | = 0
=> x = \(\frac{1}{2}\)
Vậy MaxA = 0 <=> x = \(\frac{1}{2}\)
b)
\(-\left|5x-3\right|\le0\forall x\Rightarrow4-\left|5x-3\right|\le4\)
Dấu " = " xảy ra khi :
- | 5x - 3 | = 0
=> x = \(\frac{3}{5}\)
Vậy MaxB = 4 <=> x = \(\frac{3}{5}\)
Study well

a, Có \(\left(x^2-9\right)^2\)≥0 ∀ x ∈ Z
|y-2| ≥0 ∀ y ∈ Z
⇒ Gía trị nhỏ nhất A=-1. Dấu ''='' xảy ra khi:\(\left(x^2-9\right)^2\)+|y-2|=0
⇒ \(x=3\) ; \(y=2\)
Vậy.....
b, Có \(x^4\) ≥ 0 ∀ x ∈ Z
3\(x^2\) ≥ 0 ∀ x ∈ Z
⇒ Giá trị nhỏ nhất của B=2. Dấu ''='' xảy ra khi: \(x^4\)+3\(x^2\)=0
⇒ \(x^2\left(x^2+3\right)\)=0
⇒ \(x^2\) =0
⇒ \(x=0\)
Vậy...

T/C của gttđ là >= 0 nên
a) GTNN = -4
b) GTLN = 2
c) GTNN = 2

1:
a: \(A=2+3\sqrt{x^2+1}>=3\cdot1+2=5\)
Dấu = xảy ra khi x=0
b: \(B=\sqrt{x+8}-7>=-7\)
Dấu = xảy ra khi x=-8

c) Ta có: \(\left|5x-2\right|\ge0\forall x\)
\(\left|3y+12\right|\ge0\forall y\)
Do đó: \(\left|5x-2\right|+\left|3y+12\right|\ge0\forall x,y\)
\(\Leftrightarrow-\left|5x-2\right|-\left|3y+12\right|\le0\forall x,y\)
\(\Leftrightarrow-\left|5x-2\right|-\left|3y+12\right|+4\le4\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}5x-2=0\\3y+12=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5x=2\\3y=-12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2}{5}\\y=-4\end{matrix}\right.\)
bạn làm bài nào đây ạ? 4 - |5x-2| - |3y + 12| mà đâu phải −|5x−2|−|3y+12|+4

\(A=\left(x-1\right)^2+1.\\ \left(x-1\right)^2\ge0\forall x\in R.\\ 1>0.\\ \Rightarrow\left(x-1\right)^2+1\ge1\forall x\in R.\\ \Rightarrow A\ge1.\\ \Rightarrow A_{min}=1.\)
\(B=x^2+x^4-\dfrac{1}{2}.\\ x^2+x^4\ge0\forall x\in R.\\ \Leftrightarrow x^2+x^4-\dfrac{1}{2}\ge\dfrac{-1}{2}\forall x\in R.\\ \Rightarrow B\ge\dfrac{-1}{2}.\\ \Rightarrow B_{min}=\dfrac{-1}{2}.\)
\(D=\dfrac{2}{\left(x-1\right)^2}+1.\\ \left(x-1\right)^2\ge0\forall x\in R.\\ \Leftrightarrow\dfrac{2}{\left(x-1\right)^2}\ge0.\\ \Leftrightarrow\dfrac{2}{\left(x-1\right)^2}+1\ge1\forall x\in R.\\ \Rightarrow D\ge1.\\ \Rightarrow D_{min}=1.\)

a) \(A=2,7+\left|x-1,5\right|\ge2,7\)
\(minA=2,7\Leftrightarrow x=1,5\)
b) \(B=\left|4,1+x\right|-6,3\ge-6,3\)
\(minB=-6,3\Leftrightarrow x=-4,1\)
a)
Ta có:
\(\left|x-1,5\right|\)≥0
=>\(2,7+\left|x-1,5\right|\)≥2,7
GTNN:A=2,7 khi x-1,5=0
x=1,5
Ta có:
\(\left|4,1+x\right|\)≥0
=>\(\left|4,1+x\right|-6,3\)≥-6,3
GTNN:B=6,3 khi 4,1+x=0
x=-4,1

Với mọi x ta có :
\(\left|x+5\right|\ge0\)
\(\Leftrightarrow\left|x+5\right|+5\ge0\)
\(\Leftrightarrow A\ge5\)
Dấu "=" xảy ra \(\Leftrightarrow x=-5\)
Vậy..