Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A=4x^2-12x+9-\left(x^2+6x+5\right)+2\)
\(=3x^2-18x+6\)
\(=3\left(x^2-6x+9\right)-21\)
\(=3\left(x-3\right)^2-21\ge-21\)
\(A_{min}=-21\) khi \(x=3\)

1, Ta có: 3-x2+2x=-(x2-2x+1)+4=-(x-1)2+4
vì (x-1)2 luôn lớn hơn hoặc bằng không với mọi x-->-(x-1)2 nhỏ hơn hoặc bằng 0 với mọi x
vậy giá trị lớn nhất của biểu thức 3-x2+2x là 4
các bài giá trị nhỏ nhất còn lại làm tương tự bạn nhé
chỉ cần đưa về nhân tử chung hoặc hằng đẳng thức là được

BÀI 2 a, x2+x+1=(x2+1/2*2*x+1/4)-1/4+1=(x+1/2)2 +3/4
MÀ (x+1/2)2>=0 với mọi giá trị của x .Dấu"=" xảy ra khi x+1/2=0 =>x=-1/2
=>(x+1/2)2+3/4>=3/4 với mọi giá trị của x .Dấu "=" xảy ra khi x=-1/2
=>x2+x+1 có giá trị nhỏ nhất là 3/4 khi x=-1/2
b,A=y(y+1)(y+2)(y+3)
=>A =[y(y+3)] [(y+1)(y+2)]
=>A=(y2+3y) (y2+3y+2)
Đặt X=y2+3y+1
=>A=(X+1)(X-1)
=>A=X2-1
=>A=(y2+3y+1)2-1
MÀ (y2+3y+1)2>=0 với mọi giá trị của y
=>(y2+3y+1)2-1>=-1
Vậy GTNN của Alà -1
c,B=x3+y3+z3-3xyz
=>B=(x3+y3)+z3-3xyz
=>B=(x+y)3-3xy(x+y)+z3-3xyz
=>B=[(x+y)3+z3]-3xy(x+y+z)
=>B=(x+y+z)(x2+2xy+y2-xz-yz+z2)-3xy(x+y+z)
=>B=(x+y+z)(x2+2xy+y2-xz-yz+z2-3xy)
=>B=(x+y+z)(x2+y2+z2-xy-xz-yz)

b: Tham khảo:
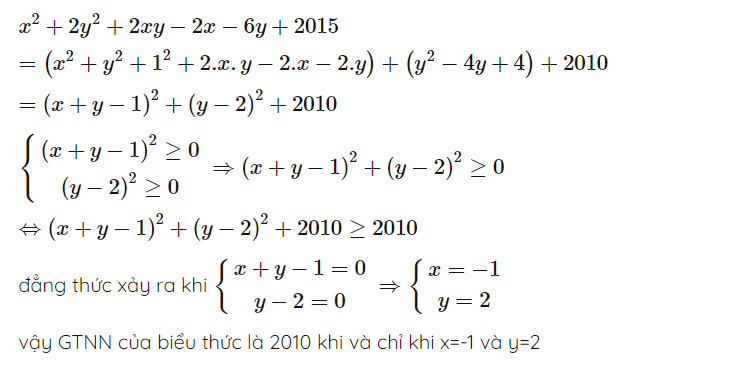
a: \(P=x^2-5x+\dfrac{25}{4}-\dfrac{25}{4}=\left(x-\dfrac{5}{2}\right)^2-\dfrac{25}{4}\ge-\dfrac{25}{4}\forall x\)
Dấu '=' xảy ra khi x=5/2

1:
ĐKXĐ: \(x\notin\left\{3;-2;1\right\}\)
\(A=\left(\dfrac{x\left(x+2\right)-x+1}{\left(x-3\right)\left(x+2\right)}\right):\left(\dfrac{x\left(x-3\right)+5x+1}{\left(x+2\right)\left(x-3\right)}\right)\)
\(=\dfrac{x^2+2x-x+1}{\left(x-3\right)\left(x+2\right)}\cdot\dfrac{\left(x+2\right)\left(x-3\right)}{x^2-3x+5x+1}\)
\(=\dfrac{x^2+x+1}{\left(x-1\right)^2}\)
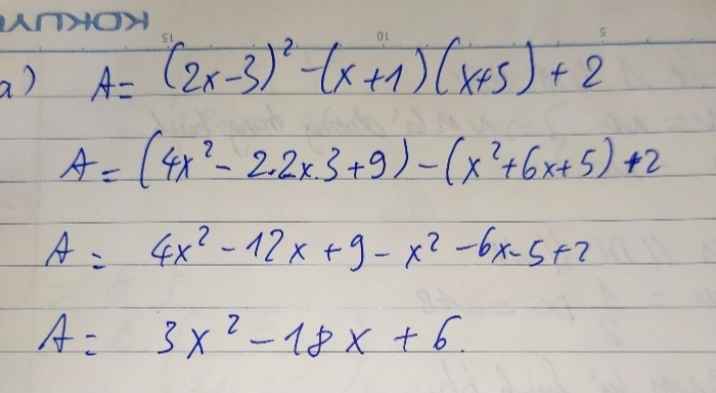

Ta có: A = (x + 2)(x - 3) + x(x - 1) - 4 = x2 - 3x + 2x - 6 + x2 - x - 4 = 2x2 - 2x - 10 = 2(x2 - x + 1/4) - 21/2 = 2(x - 1/2)2 - 21/2
Ta luôn có: 2(x - 1/2)2 \(\ge\)0 \(\forall\)x
=> 2(x - 1/2)2 - 21/2 \(\ge\)-21/2 \(\forall\)x
hay A \(\ge\)-21/2 \(\forall\)x
Dấu "=" xảy ra <=> x -1/2 = 0 <=> x = 1/2
vậy Min của A = -21/2 tại x = 1/2
\(A=\left(x+2\right)\left(x-3\right)+x\left(x-1\right)-4\)
\(\Leftrightarrow A=x^2-x-6+x^2-x-4\)
\(\Leftrightarrow A=2x^2-2x-10\)
\(\Leftrightarrow A=2\left(x^2-x-5\right)\)
\(\Leftrightarrow A=2\left(x^2-2.\frac{1}{2}x+\frac{1}{4}-\frac{21}{4}\right)\)
\(\Leftrightarrow A=2\left[\left(x-\frac{1}{2}\right)^2-\frac{21}{4}\right]\)
\(\Leftrightarrow A=2\left[\left(x-\frac{1}{2}\right)^2\right]-\frac{42}{4}\ge-\frac{42}{4}\)
Vậy \(A_{min}=\frac{-42}{4}\Leftrightarrow x=\frac{1}{2}\)