Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y=\left|x^2-2x-m\right|=-x^2+2x+m\)
\(\left(nếu:x^2-2x-m< 0\right)\)
\(f\left(x\right)=-x^2+2x+m\Rightarrow x=\dfrac{-b}{2a}=1\in\left[-3;2\right]\)
\(f\left(-3\right)=m-15\)
\(f\left(1\right)=m+1\)
\(f\left(2\right)=m\Rightarrow f\left(-3\right)< f\left(2\right)< f\left(1\right)\)
\(\Rightarrow max_{f\left(x\right)}=m+1=10\Leftrightarrow m=9\)
\(do..m< 0\Rightarrow m=9\left(ktm\right)\)
\(\Rightarrow không\) \(có\) \(giá\) \(trị\) \(m\) \(thỏa\)

\(h\left(x\right)=x^2-4x+5+m\)
\(g\left(x\right)=\left|h\left(x\right)\right|=\left|f\left(x\right)+m\right|=\left|x^2-4x+5+m\right|\)
\(h\left(0\right)=5+m;h\left(4\right)=5+m;h\left(2\right)=1+m\)
TH1: \(1+m>0\Leftrightarrow m>-1\)
\(max=5+m=9\Leftrightarrow m=4\left(tm\right)\)
TH2: \(5+m< 0\Leftrightarrow m< -5\)
\(max=-1-m=9\Leftrightarrow m=-10\left(tm\right)\)
TH3: \(5+m>0>1+m\Leftrightarrow-5< m< -1\)
Nếu \(5+m< -1-m\Leftrightarrow m< -3\)
\(max=-1-m=9\Leftrightarrow m=-10\left(tm\right)\)
Nếu \(5+m=-1-m\Leftrightarrow m=-3\)
\(max=5+m=2\ne9\)
\(\Rightarrow m=-3\) không thỏa mãn yêu cầu bài toán
Nếu \(5+m>-1-m\Leftrightarrow m>-3\)
\(max=5+m=9\Leftrightarrow m=4\left(tm\right)\)
Vậy \(m=4;m=-10\)

y = (x² - 1)(x + 3)(x + 5)
= [(x - 1)(x + 5)].[(x + 1)(x + 3)]
= (x² + 4x - 5)(x² + 4x + 3)
= [x² + 4x - 1) - 4].[(x² + 4x - 1) + 4]
= (x² + 4x - 1)² - 16 ≥ - 16
- Khi x = 0 ⇒ y = - 15
- Khi x = 1 ⇒ y = 0
- Khi x² + 4x - 1 = 0 ⇔ x = √5 - 2 ( loại giá trị x = - √5 - 2 < 0) ⇒ y = - 16
Vậy trên đoạn [0; 1] thì :
GTNN của y = - 16 khi x = √5 - 2
GTLN của y = 0 khi x = 1

Lời giải:
$x^2-2x-3=x(x+3)-5(x+3)+12=(x+3)(x-5)+12$
Vì $x\in [-3;4]$ nên $x+3\geq 0; x-5< 0$
$\Rightarrow x^2-2x-3=(x+3)(x-5)+12\leq 12$
Vậy GTLN của hàm số là $12$ khi $x=-3$

b, \(\left\{{}\begin{matrix}x^2-2x-3\le0\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1\le x\le3\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)
Yêu cầu bài toán thỏa mãn khi phương trình \(f\left(x\right)=x^2-2mx+m^2-9\ge0\) có nghiệm \(x\in\left[-1;3\right]\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=m^2-m^2+9=9>0,\forall m\\-1< m< 3\\f\left(-1\right)=m^2+2m-8\ge0\\f\left(3\right)=m^2-6m\ge0\end{matrix}\right.\)
\(\Leftrightarrow m\in[2;3)\cup(-1;0]\)

TA có: \(y=-x^4+4x^2-3\)
\(=-\left(x^4-4x^2+4\right)+1\)
\(=-\left(x^2-1\right)^2+1\le1\)
Vì \(y\in\left[-2;3\right]\)
=>..........................
Đến đây dễ rồi bạn tự làm nốt nhé
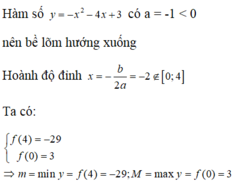
\(y=f\left(x\right)=x^2-2x+3\)
\(f\left(0\right)=3;f\left(4\right)=11;f\left(1\right)=2\)
\(\Rightarrow max=f\left(4\right)=11\Leftrightarrow x=4\)