Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
(1 + x)3 + (1 - x)3 - 6x(x + 1) = 6
<=> x3 + 3x2 + 3x + 1 - x3 + 3x2 - 3x + 1 - 6x2 - 6x = 6
<=> -6x + 2 = 6
<=> -6x = 6 - 2
<=> -6x = 4
<=> x = -4/6 = -2/3
Bài 3:
a) (7x - 2x)(2x - 1)(x + 3) = 0
<=> 10x3 + 25x2 - 15x = 0
<=> 5x(2x - 1)(x + 3) = 0
<=> 5x = 0 hoặc 2x - 1 = 0 hoặc x + 3 = 0
<=> x = 0 hoặc x = 1/2 hoặc x = -3
b) (4x - 1)(x - 3) - (x - 3)(5x + 2) = 0
<=> 4x2 - 13x + 3 - 5x2 + 13x + 6 = 0
<=> -x2 + 9 = 0
<=> -x2 = -9
<=> x2 = 9
<=> x = +-3
c) (x + 4)(5x + 9) - x2 + 16 = 0
<=> 5x2 + 9x + 20x + 36 - x2 + 16 = 0
<=> 4x2 + 29x + 52 = 0
<=> 4x2 + 13x + 16x + 52 = 0
<=> 4x(x + 4) + 13(x + 4) = 0
<=> (4x + 13)(x + 4) = 0
<=> 4x + 13 = 0 hoặc x + 4 = 0
<=> x = -13/4 hoặc x = -4

TXĐ: \(\left\{{}\begin{matrix}x\in R\\x\notin\left\{-3;1\right\}\end{matrix}\right.\)
Để giá trị 2 biểu thức bằng nhau thì \(\dfrac{x+2}{x+3}-\dfrac{x+1}{x-1}=\dfrac{4}{\left(x+3\right)\left(x-1\right)}\)
\(\Leftrightarrow\dfrac{\left(x+2\right)\left(x-1\right)}{\left(x+3\right)\left(x-1\right)}-\dfrac{\left(x+1\right)\left(x+3\right)}{\left(x-1\right)\left(x+3\right)}=\dfrac{4}{\left(x+3\right)\left(x-1\right)}\)
Suy ra: \(x^2-x+2x-2-\left(x^2+4x+3\right)=4\)
\(\Leftrightarrow x^2+x-2-x^2-4x-3-4=0\)
\(\Leftrightarrow3x-9=0\)
\(\Leftrightarrow3x=9\)
hay x=3(thỏa ĐK)
Vậy: S={3}

T a c ó : A = B ⇔ ( x – 1 ) ( x 2 + x + 1 ) – 2 x = x ( x – 1 ) ( x + 1 ) ⇔ x 3 – 1 – 2 x = x ( x 2 – 1 ) ⇔ x 3 – 1 – 2 x = x 3 – x ⇔ x 3 – x 3 – 2 x + x = 1 ⇔ - x = 1 ⇔ x = - 1 V ậ y v ớ i x = - 1 t h ì A = B

Điều kiện: 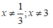
Để biểu thức đã cho có giá trị bằng 2 thì:
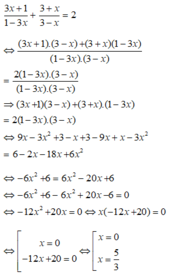
Kết hợp điều kiện phương trình đã cho có 2 nghiệm là x = 0 và x = 5 3
Chọn đáp án A

Điều kiện:
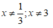
Để biểu thức đã cho có giá trị bằng 2 thì:
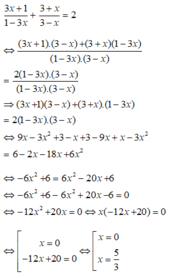
Kết hợp điều kiện phương trình đã cho có 2 nghiệm là x = 0 và x = 5 3
Chọn đáp án A

a) ( x - 2 ) . ( x + 2 ) - ( x - 1 ) ^ 3 - x ^ 2 . ( 4 - x )
= x ^ 2 - 4 - x ^ 3 + 3 x ^ 2 - 3 x + 1- 4 x ^ 2 + x ^ 3
= - 3 - 3 x
= - 3 . ( 1 + x )
b) để biểu thức A nhận giá trị bằng 0 thì: 3 . ( 1 + x ) = 0 <=> x = - 1
:-) => cre~
A = B ⇔(x – 1)(x2 + x + 1) – 2x = x(x – 1)(x + 1) + 2x – 3
⇔ x3 – 1 – 2x = x(x2 – 1) + 2x – 3
⇔ x3 – 1 – 2x = x3 – x + 2x – 3
⇔ -3x = -2 ⇔ x = 2/3 .