K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
13 tháng 2 2019
Giả sử hai đường thẳng ( d 1 ): 5x – 2y = 3; ( d 2 ): x + y = m cắt nhau tại điểm A(x, y).
Vì giao điểm A nằm trên trục Oy nên x = 0. Suy ra: A(0; y).
Khi đó điểm A(0; y) là nghiệm của hệ phương trình: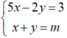 
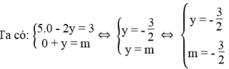
Vậy khi m = - 3/2 thì ( d 1 ): 5x – 2y = 3; (d2): x + y = m cắt nhau tại một điểm trên trục Oy.
Phương trình đường thẳng ( d 2 ): x + y = - 3/2
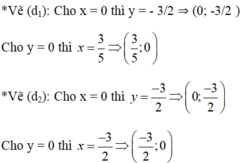
Đồ thị:
23 tháng 10 2021
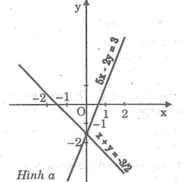
b: Phương trình hoành độ giao điểm là:
x+1=-x+3
\(\Leftrightarrow2x=2\)
\(\Leftrightarrow x=1\)
hay y=2
CM
24 tháng 12 2018
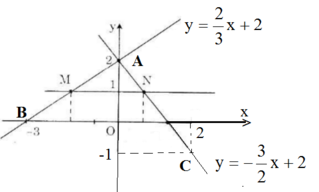
b) Điểm M có tung độ y = 1 nên hoành độ là
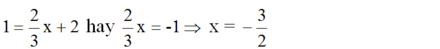
Điểm N có tung độ y = 1 nên hoành độ là
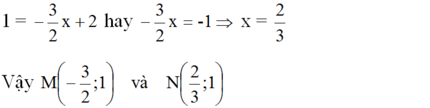
Giả sử hai đường thẳng ( d 1 ): mx + 3y = 10; ( d 2 ): x – 2y = 4 cắt nhau tại điểm B(x, y).
Vì điểm B nằm trên trục Ox nên y = 0 ⇒ B( x, 0).
Khi đó điểm B(x; 0) là nghiệm của hệ phương trình: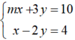
Vậy khi m = 5/2 thì ( d 1 ): mx + 3y = 10; ( d 2 ): x – 2y = 4 cắt nhau tại một điểm trên trục Ox.
Phương trình đường thẳng (d1):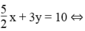
5x + 6y = 20
*Vẽ ( d 1 ): Cho x = 0 thì y = 10/3 ⇒ (0; 10/3 )
Cho y = 0 thì x = 4 ⇒ (4; 0)
*Vẽ ( d 2 ): x - 2y = 4. Cho x = 0 thì y = -2 ⇒ (0; -2)
Cho y = 0 thì x = 4 ⇒ (4; 0)
Đồ thị: