Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: m - 1 x + 6 ≥ 0 ; x + 2 ≥ 0 . Do đó,
m - 1 x + 6 + x + 2 = 0 ⇔ m - 1 x + 6 = 0 x + 2 = 0 ⇔ m - 1 . - 2 + 6 = 0 x = - 2 ⇔ - 2 m + 2 + 6 = 0 x = - 2 ⇔ m = 4 x = - 2
Chọn A.

+ Khi m = 0, bất phương trình trở thành - 2 x + 2 < 0 ⇔ x > 1 . Vậy m = 0 không thỏa mãn yêu cầu của bài toán.
+ Khi m ≠ 0 , bất phương trình vô nghiệm khi m x 2 + 2 m - 1 x + m + 2 ≥ 0 , ∀ x ∈ ℝ . ⇔ a > 0 ∆ ' ≤ 0 ⇔ m > 0 ( m - 1 ) 2 - m ( m + 2 ) ≤ 0 .
⇔ m > 0 - 4 m + 1 ≤ 0 ⇔ m > 0 m ≥ 1 4 ⇔ m ≥ 1 4
Chọn C.


Ta có f x ≥ 0 ⇔ x + 3 m ≥ 2 ⇔ x ≥ 2 - 3 m
f x ≥ 0 với mọi x ∈ [ 1 ; + ∞ ) ⇔ [ 1 ; + ∞ ) ⊂ [ 2 - 3 m ; + ∞ ) ⇔ 2 - 3 m ≤ 1 ⇔ m ≥ 1 3 .
Chọn C.

Hàm số y = ax + b ( a ≠ 0 ) đồng biến trên R khi a> 0.
Do đó, để hàm số đã cho đồng biến trên R thì m 2 - 1 > 0 ⇔ [ m > 1 m < - 1
Chọn C.

Điều kiện xác định: 2 x - 3 ≥ 0 4 x - 3 ≥ 0 ⇔ x ≥ 3 2 x ≥ 3 4 ⇔ x ≥ 3 2
Tập xác định của hàm số là [ 3 2 ; + ∞ )

x - y = m ( 1 ) x 2 - x y - m - 2 = 0 ( 2 )
Từ (1), ta có y = x - m , thế vào (2) ta được phương trình:
x2 – x (x- m) – m - 2= 0 ⇔ x2 – x2 + mx –m –2 = 0
hay mx –m -2 = 0 (*) .
Hệ phương trình đã cho có nghiệm khi phương trình (*) có nghiệm ⇔ m ≠ 0 .
Chọn B.
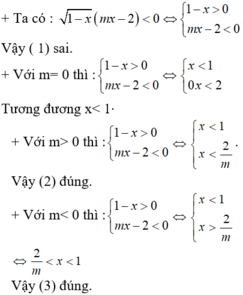
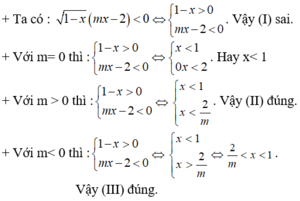
Hàm số y = m - 2 x - x + 1 xác định khi và chỉ khi m - 2 x ≥ 0 x + 1 ≥ 0 ⇔ x ≤ m 2 x ≥ - 1 .
Do đó tập xác định của hàm số y = m - 2 x - x + 1 là một đoạn trên trục số khi và chỉ khi m 2 > - 1 ⇔ m > - 2