Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
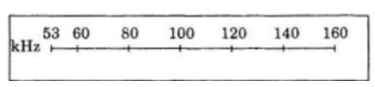
a) Theo giả thiết ta có: d = 0 => F = 53 <=> k.a0=53 <=> k = 53
Và d = 12 => F = 160 <=> k.a12=160
c) Từ câu b) => d = 25,119.lgF-43,312
(do yêu cầu kết quả tính chính xác đến hàng phần trăm)
Vậy ta có bảng.
| F | 53 | 60 | 80 | 100 | 120 | 140 | 160 |
| d | 0 | 1,35 | 4,49 | 6,93 | 8,91 | 10,60 | 12 |
a) 
. Tập xác định : R 
{
} ;
và 
;
Do đó hàm số luôn đồng biến trên mỗi khoảng xác định của nó.
b) Tiệm cận đứng ∆ : x = .
A(-1 ;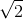 
) ∈ ∆ ⇔ = -1 ⇔ m = 2.
c) m = 2 =>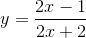 
.
a) . Tập xác định : R {} ;
và ;
Do đó hàm số luôn đồng biến trên mỗi khoảng xác định của nó.
b) Tiệm cận đứng ∆ : x = .
A(-1 ; 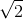) ∈ ∆ ⇔ = -1 ⇔ m = 2.
c) m = 2 => .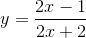
Theo mik là thế này , mik ko chắc cho lắm
Bài giải:
Theo như bảng biến thiên bạn nhận thấy được cực tiểu là 0 và giá trị cực đại của hàm số là 3.
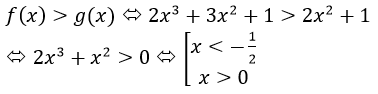
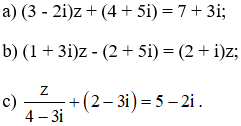
viết sai hết rồi bạn ơi