Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có thể tìm các bội của một số khác 0 bằng cách nhân số đó lần lược cho 1, 2, 3, …
Ví dụ :
B(5) = {5.1, 4.2, 5.3, …} = {5, 10, 15, …}
Ta có thể tìm các ước của một số a (a > 1) bằng cách lần lược chia số a cho số tự nhiên từ 1 đến a để xét xem a chia hết cho những số nào, khi đó các số ấy là ước của a.

1.
Để 5a8 chia hết cho 3 thì (5 + 8 + a) phải chia hết cho 3
Hay 13 + a chia hết cho 3
=> a = 2; 5; 8
2.
Để 34a chia hết cho 3 và 5 thì a = 0 hoặc a = 5
+) a = 0 ta có số: 340 (Loại vì 3 + 4 + 0 không chia hết cho 3)
+) a = 5 ta có số: 345 (Thỏa mãn yêu cầu)
Vậy a = 5
3. Gọi chữ a hàng nghìn là a1, chữ a hàng đơn vị là a2
Để a26a chia hết cho 5 thì a2 = 0 hoặc a2 = 5
+) a2 = 0 thì a26a = a260
=> a1 + 2 + 6 + 0 chia hết cho 9
hay 8 + a1 chia hết cho 9
=> a1 = 1
+) a2 = 5 thì a26a = a265
=> a1 + 2 + 6 + 5 chia hết cho 9
hay 13 + a1 chia hết cho 9
=> a1 = 5
Vậy a26a = 1260; 5265
4. Gọi chữ a hàng nghìn là a1, chữ a hàng đơn vị là a2
Để a34a chia hết cho 2 và 5 thì a2 = 0
Ta có số: a340
Để a340 chia hết cho 3 và 9 thì a1 + 3 + 4 + 0 chia hết cho 9
hay a1 + 7 chia hết cho 9
=> a1 = 2
Vậy a34a = 2340

B1/
Không có giá trị * nào thỏa mãn 457* chia hét cho cả 2, 3, 5 và 9 vì:
- Để 457* chia hết cho 2 và 5 thì * phải bằng 0 (* phải cố định là 0)
- Mà 457* còn phải chia hết cho 3 và 9 mà số 4570 không chia hết cho 3 và 9
Vậy không có giá trị * thỏa mãn
B2/
a/ Để 3a78b chia hết cho 2 và 5 thì chữ số cuối phải bằng 0, tức b = 0
Để 3a780 chia hết cho 3 và 9 thì 3a780 phải chia hết cho 9
Mà 3 + a + 7 + 8 + 0 = 18 + a suy ra a = 0 hoặc a = 9
Vậy hai số tìm được là: 30780 hoặc 39780
b/ Để 4a5b chia hết cho 2 và 5 nên chữ số cuối tức b = 0
Để 4a50 chia hết cho 3 nhưng không chia hết cho 9 thì
4 + a + 5 + 0 = 9 + a chia hết cho 3 không chia hết cho 9
Suy ra a = 3 hoặc a = 6
Vậy hai số tìm được là 4350 hoặc 4650

a, Vì 12ab chia hết co cả 2 và 5 nên => b = 0
Thay vào, ta có 12a0 chia hết cho 3 khi và chỉ khi 1 + 2 + a + 0 chia hết cho 3 => 3 + a chia hết cho 3
=> a thuộc { 0; 3; 6; 9 }
b, Vì a47b chia hết cho 2, 5 nên => b = 0
Thay vào, ta thấy a470 chia hết cho 9 khi và chỉ khi a + 4 + 7 + 0 chia hết cho 9 => a + 11 chia hết cho 9
=> a = 7
c, Vì 7a3b chia hết cho 5 nên => b = 0 hoặc b = 5
Nếu b = 0 thì a thuộc { 2; 5; 8 }
Nếu b = 5 thì a thuộc { 0; 3; 6; 9 }
d, Vì 4a9b chia hết cho 5 nên b = 0, hoặc b = 5
Nếu b = 5 thì a thuôc { 0; 9 }
Nếu b = 0 thì a = 5
1) do 12ab chia hết cho cả 2 và 5 nên b=0
Mà 12ab chia hết cho 3 nên 1+2+a+b=3+a+0 chia hết cho 3
nên a=3; a=6; a=9.
2) Làm tương tự câu 1
3)do 7a3b chia hết cho 5 nên b=0 hoặc b=5
Nếu b=0=>a+7+3+0 chia hết cho 3(4a3b chia hết cho 3)
nên a=2; a=5; a=8
Nếu b=5=>a+7+3+5 chia hết cho 3
nên a=3; a=6; a=9
4) làm tương tự câu 3

a) * = x
=> các số chia hết cho 2 và 5 đều là các số có chữ số tận cùng là : 0
=> x = 0 tương ứng với *=0
b) * = x
=> các số chia hết cho 9 là các số có tổng các chữ số chia hết cho 9
các số chia hết cho 2 và 5 đều là các số có chữ số tận cùng là : 0
các số chia hết cho 3 là tổng các chữ số chia hết cho 3
=> TH chia hết cho 9 : 45x = 0;9
=> TH chia hết cho 2,5 : 45x = 0
=> TH chia hết cho 3: 45x = 0;3;6;9
=> số chung trong các TH là : 0 . Vậy x = 0 tương ứng với *=0
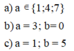
a)486
b)5790 hoặc 5760 và 5730
c)4050 hoặc 4950
d)7875