NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
2
15 tháng 3 2019
xy . yz . zx = (-18).48.(-24)
x2y2z2 = 20736
xyz = \(\sqrt{20736}\)= 144
=> z = \(\frac{xyz}{xy}=\frac{144}{-18}=-8\)
x = \(=\frac{xyz}{yz}=\frac{144}{48}=3\)
y = \(\frac{xyz}{xz}=\frac{144}{-24}=-6\)
vậy ...
KN
15 tháng 3 2019
Giải
Theo đề bài, ta có: \(\hept{\begin{cases}xy=-18\\yz=48\\zx=-24\end{cases}\Rightarrow\left(xy\right).\left(yz\right).\left(zx\right)=\left(-18\right).48.\left(-24\right)}\)
\(\Leftrightarrow x^2y^2z^2=20736\)
\(\Leftrightarrow\left(xyz\right)^2=20736\)
\(\Leftrightarrow xyz=\pm144\)
\(TH1:xyz=-144\)
\(\Rightarrow\hept{\begin{cases}z=-144\div\left(-18\right)=8\\x=-144\div48=-3\\y=-144\div\left(-24\right)=6\end{cases}}\)
\(TH2:xyz=144\)
\(\Rightarrow\hept{\begin{cases}z=144\div\left(-18\right)=-8\\x=144\div48=3\\y=144\div\left(-24\right)=-6\end{cases}}\)
HV
0
TH
2
5 tháng 4 2015
Do x; y ; z > 0 nên xyz khác 0 => \(\frac{xy}{xyz}+\frac{yz}{xyz}+\frac{zx}{xyz}=1\Rightarrow\frac{1}{z}+\frac{1}{x}+\frac{1}{y}=1\Rightarrow\frac{1}{x}1\)
Vì x<= y< = z nên \(\frac{1}{x}\ge\frac{1}{y}\ge\frac{1}{z}\Rightarrow\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\le\frac{1}{x}+\frac{1}{x}+\frac{1}{x}=\frac{3}{x}\)
=> 1 < = 3/x => x < = 3 mà x > 1 nên x = 2 hoặc 3
Nếu x = 2 => \(\frac{1}{y}+\frac{1}{z}=\frac{1}{2}\Rightarrow\frac{1}{y}2;\frac{1}{y}+\frac{1}{z}\le\frac{2}{y}\Rightarrow\frac{2}{y}\ge\frac{1}{2}\Rightarrow y\le4\)
mà y >2 => y = 3 hoặc 4
y = 3 => z = 6;
y = 4 => z = 4
nếu x = 3 => \(\frac{1}{y}+\frac{1}{z}=\frac{2}{3}\Rightarrow\frac{1}{y}\frac{3}{2};\frac{1}{y}+\frac{1}{z}\le\frac{2}{y}\Rightarrow\frac{2}{y}\ge\frac{2}{3}\Rightarrow y\le3\)
theo đề bài x<= y nên y = 3 => z = 3
Vậy (x;y;z) = (3;3;3); (2;3;6);(2;4;4)
TQ
2
30 tháng 7 2016
\(xy=-30\Rightarrow\frac{x}{-30}=\frac{1}{y}\)
\(yz=42\Rightarrow\frac{z}{42}=\frac{y}{1}\)
\(\Rightarrow\frac{x}{30}=\frac{z}{42}\)
Áp dụng tính chất dãy tỉ số bằng nhau :
\(\frac{x}{-30}=\frac{z}{42}=\frac{z-x}{42-\left(-30\right)}=-\frac{12}{72}=-\frac{1}{6}\)
\(\frac{x}{-30}=\frac{1}{-6}\Rightarrow x=5\)
\(\frac{z}{42}=-\frac{1}{6}\Rightarrow z=-7\)
Ta có xy = -30
=> y = -30 : x = -30 : 5 = -6
Vậy y = -6; x = 5 ; z= -7
30 tháng 7 2016
ta có xy=-30=>. x=-30/y
yz=42=> z=42/y
thay vào z-x=-12 ta được :\(\frac{42}{y}+\frac{30}{y}=-12\)
<=> y=-6
ta có y=-6=> x=-30/-6=5
y=-6=>z=42/-6=-7
vậy (x,y,z) là (5;-6;-7)
PT
1
LM
0
VT
0
H
0
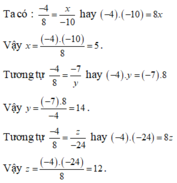
ta có x, y , z, t # 0
lấy y.t : y.z = 48/24 = 2
hay t = 2.z kết hợp điều này với t.z = 32 ta sẽ có
t = 4 vậy z =8, y = 3 , x =4
t = -4. z = -8 , y = -3 , x= -4