K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
0
10 tháng 9 2021
Bài 2:
a: Ta có: \(2^{x+1}\cdot3^y=12^x\)
\(\Leftrightarrow2^{x+1}\cdot3^y=2^{2x}\cdot3^x\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+1=2x\\x=y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
17 tháng 4 2021
a,(2x+1)(y-3)=12
⇒⇒2x+1 và y-3 ∈∈Ư(12)={±1;±2;±3;±4;±6;±12}{±1;±2;±3;±4;±6;±12}
| 2x+1 | 1 | -1 | 2 | -2 | 3 | -3 |
| y-3 | 12 | -12 | 6 | -6 | 4 | -4 |
| x | 0 | -1 | 1212 | −32−32 | 1 | -2 |
| y | 15 | -9 | 9 | 3 | 7 | -1 |
=>x=0,y=15
17 tháng 4 2021
c) Ta có: \(36^{25}=\left(6^2\right)^{25}=6^{50}\)
\(25^{36}=\left(5^2\right)^{36}=5^{72}\)
Ta có: \(6^{50}=\left(6^5\right)^{10}=7776^{10}\)
mà \(5^{70}=\left(5^7\right)^{10}=78125^{10}\)
nên \(6^{50}< 5^{70}\)
mà \(5^{70}< 5^{72}\)
nên \(6^{50}< 5^{72}\)
hay \(36^{25}< 25^{36}\)
GL
1
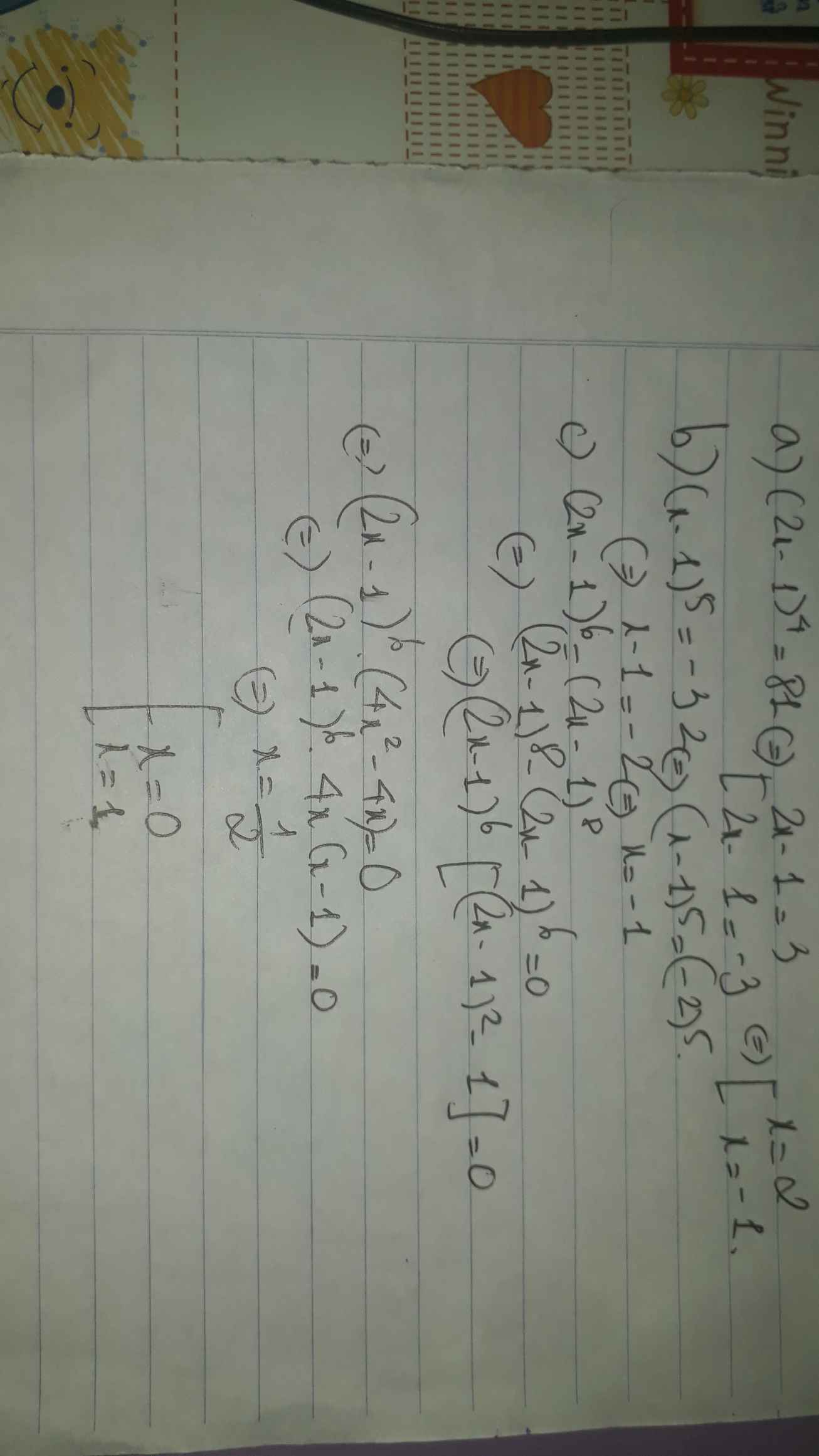
Đặt A=(2x+1)(2x+2)(2x+3)(2x+4)
Ta có: 2x⋅Alà tích của 5 số tự nhiên liên tiếp nên 2x⋅A⋮5
Nhưng 2x⋮̸ 5, do đó A⋮5
Nếu y≥1y≥1, ta có (2x+1)(2x+2)(2x+3)(2x+4)−5y⋮5
Mà 11879⋮̸ 5⇒y≥1 không thỏa mãn suy ra y=0
Khi đó pt⇔(2x+1)(2x+2)(2x+3)(2x+4)−1=11879
⇔(2x+1)(2x+2)(2x+3)(2x+4)=11880
⇔(2x+1)(2x+2)(2x+3)(2x+4)=9⋅10⋅11⋅12⇔x=3
Vậy {x=3
y=0 là 2 số tự nhiên cần tìm